
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() 且
且![]() ,点
,点![]() 在椭圆内部,点
在椭圆内部,点![]() 在椭圆上,则以下说法正确的是( )
在椭圆上,则以下说法正确的是( )
A.![]() 的最小值为
的最小值为![]()
B.椭圆![]() 的短轴长可能为2
的短轴长可能为2
C.椭圆![]() 的离心率的取值范围为
的离心率的取值范围为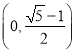
D.若![]() ,则椭圆
,则椭圆![]() 的长轴长为
的长轴长为![]()
 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:
【题目】《周髀算经》是中国古代重要的数学著作,其记载的“日月历法”曰:“阴阳之数,日月之法,十九岁为一章,四章为一部,部七十六岁,二十部为一遂,遂千百五二十岁,….生数皆终,万物复苏,天以更元作纪历”,某老年公寓住有20位老人,他们的年龄(都为正整数)之和恰好为一遂,其中年长者已是奔百之龄(年龄介于90至100),其余19人的年龄依次相差一岁,则年长者的年龄为( )
A.94B.95C.96D.98
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,ABCD为菱形,
中,ABCD为菱形,![]() 平面ABCD,连接AC,BD交于点O,
平面ABCD,连接AC,BD交于点O,![]() ,
,![]() ,E是棱PC上的动点,连接DE.
,E是棱PC上的动点,连接DE.
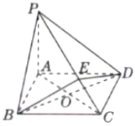
(1)求证:平面![]() 平面
平面![]() ;
;
(2)当![]() 面积的最小值是4时,求此时点E到底面ABCD的距离.
面积的最小值是4时,求此时点E到底面ABCD的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,直线
轴正半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,经过点
,经过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的倾斜角.
的倾斜角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】试在①![]() ,②
,②![]() ,③
,③![]() 三个条件中选两个条件补充在下面的横线处,使得
三个条件中选两个条件补充在下面的横线处,使得![]() 面ABCD成立,请说明理由,并在此条件下进一步解答该题:
面ABCD成立,请说明理由,并在此条件下进一步解答该题:
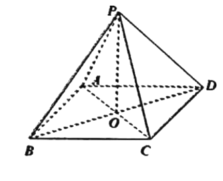
如图,在四棱锥![]() 中,
中,![]() ,底ABCD为菱形,若__________,且
,底ABCD为菱形,若__________,且![]() ,异面直线PB与CD所成的角为
,异面直线PB与CD所成的角为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线![]() 的焦点为
的焦点为![]() ,点
,点![]() 是
是![]() 上一点,且线段
上一点,且线段![]() 的中点坐标为
的中点坐标为![]() .
.
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)若![]() ,
,![]() 为抛物线
为抛物线![]() 上的两个动点(异于点
上的两个动点(异于点![]() ),且
),且![]() ,求点
,求点![]() 的横坐标的取值范围.
的横坐标的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图(1),在等腰直角![]() 中,斜边
中,斜边![]() ,D为
,D为![]() 的中点,将
的中点,将![]() 沿
沿![]() 折叠得到如图(2)所示的三棱锥
折叠得到如图(2)所示的三棱锥![]() ,若三棱锥
,若三棱锥![]() 的外接球的半径为
的外接球的半径为![]() ,则
,则![]() _________.
_________.
图(1) 图(2)
图(2) 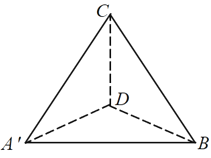
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1为菱形,D为AB的中点,![]() 为等腰三角形,∠ACB=
为等腰三角形,∠ACB=![]() ,∠ABB1=
,∠ABB1=![]() ,且AB=B1C.
,且AB=B1C.
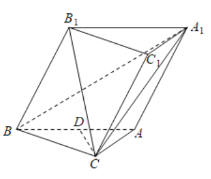
(1)证明:CD⊥平面ABB1A1 ;
(2)求CD与平面A1BC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com