
已知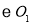 和
和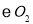 相交于A、B两点,过A点作
相交于A、B两点,过A点作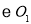 切线交
切线交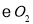 于点E,连接EB并延长交
于点E,连接EB并延长交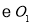 于点C,直线CA交
于点C,直线CA交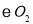 于点D,
于点D,
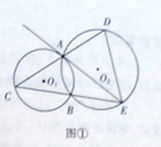
(1)当点D与点A不重合时(如图1),证明:ED2=EB·EC;
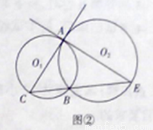
(2)当点D与点A重合时(如图2),若BC=2,BE=6,求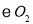 的直径长.
的直径长.
(1)证明详见解析;(2)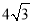
【解析】
试题分析:(1)连接AB,在EA的延长线上取点F,由弦切角定理可得∠FAC=∠ABC,而∠FAC=∠DAE,(对顶角)证得∠ABC=∠DAE,然后内接四边形的性质证得∠ABC=∠ADE,即得∠DAE=∠ADE.所以EA=ED,由切割线定理可得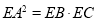 ,即
,即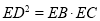 .
.
(2)直线CA与⊙O2只有一个公共点,所以直线CA与⊙O2相切,由弦切角定理知: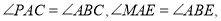 然后证明
然后证明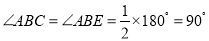 ,即AC与AE分别为⊙O1和⊙O2的直径.最后根据切割线定理证得AE的长.
,即AC与AE分别为⊙O1和⊙O2的直径.最后根据切割线定理证得AE的长.
试题解析:(1)连接AB,在EA的延长线上取点F,如图①所示.
∵AE是⊙O1的切线,切点为A,
∴∠FAC=∠ABC,.∵∠FAC=∠DAE,
∴∠ABC=∠DAE,∵∠ABC是⊙O2内接四边形ABED的外角,
∴∠ABC=∠ADE,∴∠DAE=∠ADE.∴EA=ED,∵ ,∴
,∴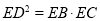

(2)当点D与点A重合时,直线CA与⊙O2只有一个公共点,
所以直线CA与⊙O2相切.如图②所示,由弦切角定理知:


∴AC与AE分别为⊙O1和⊙O2的直径. 8分
∴由切割线定理知:EA2=BE·CE,而CB=2,BE=6,CE=8
∴EA2=6×8=48,AE=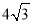 .故⊙O2的直径为
.故⊙O2的直径为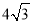 . 10分
. 10分
考点:1.弦切角定理;2.切割线定理;


科目:高中数学 来源:2013-2014学年河北省高三第一次模拟考试理科数学试卷(解析版) 题型:解答题
已知椭圆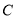 :
: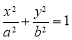 (
( )过点
)过点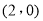 ,且椭圆
,且椭圆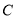 的离心率为
的离心率为 .
.
(1)求椭圆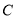 的方程;
的方程;
(2)若动点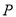 在直线
在直线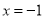 上,过
上,过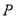 作直线交椭圆
作直线交椭圆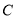 于
于 两点,且
两点,且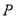 为线段
为线段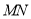 中点,再过
中点,再过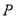 作直线
作直线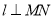 .求直线
.求直线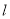 是否恒过定点,如果是则求出该定点的坐标,不是请说明理由。
是否恒过定点,如果是则求出该定点的坐标,不是请说明理由。
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省高三第一次模拟考试文科数学试卷(解析版) 题型:选择题
若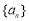 是等差数列,首项
是等差数列,首项
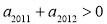 ,
,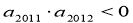 ,则使前n项和
,则使前n项和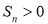
成立的最大正整数n是( )
A.2011 B.2012 C.4022 D.4023
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省石家庄市毕业班第一次模拟考试数学理科数学试卷(解析版) 题型:选择题
双曲线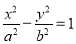 (a>0,b>0)的左右焦点分别为F1,F2,渐近线分别为l1,l2,点P在第一象限内且在l1上,若l2⊥PF1,l2∥PF2,则该双曲线的离心率为( )
(a>0,b>0)的左右焦点分别为F1,F2,渐近线分别为l1,l2,点P在第一象限内且在l1上,若l2⊥PF1,l2∥PF2,则该双曲线的离心率为( )
A. 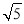 B. 2 C.
B. 2 C. 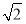 D.
D. 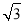
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省石家庄市毕业班第一次模拟考试数学理科数学试卷(解析版) 题型:选择题
已知a=3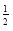 ,b=log
,b=log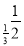 ,c=log
,c=log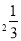 ,则( )
,则( )
A. a>b>c B.b>c>a C. c>b>ac D. b>a >c
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省石家庄市毕业班第一次模拟考试数学理文数学试卷(解析版) 题型:解答题
已知数列{an}的各项均为正数的等比数列,且a1a2=2,a3a4=32,
(1)求数列{an}的通项公式;
(2)设数列{bn}的前n项和为Sn=n2,(n∈N*),求数列{anbn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省石家庄市毕业班第一次模拟考试数学理文数学试卷(解析版) 题型:选择题
双曲线 (a>0,b>0)的左右焦点分别为F1,F2,渐近线分别为l1,l2,点P在第一象限内且在l1上,若l2⊥PF1,l2∥PF2,则该双曲线的离心率为()
(a>0,b>0)的左右焦点分别为F1,F2,渐近线分别为l1,l2,点P在第一象限内且在l1上,若l2⊥PF1,l2∥PF2,则该双曲线的离心率为()
A. B.2 C.
B.2 C.  D.
D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省唐山市高三年级第二次模拟考试理科数学试卷(解析版) 题型:解答题
在公差不为0的等差数列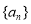 中,
中,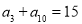 ,且
,且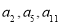 成等比数列.
成等比数列.
(1)求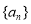 的通项公式;
的通项公式;
(2)设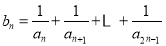 ,证明:
,证明: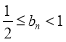 .
.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省唐山市高三年级第三次模拟考试理科数学试卷(解析版) 题型:解答题
设不等式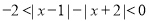 的解集为M,
的解集为M,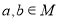 .
.
(1)证明: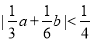 ;
;
(2)比较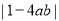 与
与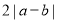 的大小,并说明理由.
的大小,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com