
【题目】已知定圆![]()
![]() ,定直线
,定直线![]()
![]() ,过
,过![]() 的一条动直线
的一条动直线![]() 与直线相交于
与直线相交于![]() ,与圆
,与圆![]() 相交于
相交于![]() ,
,![]() 两点,
两点,
(1)当![]() 与
与![]() 垂直时,求出
垂直时,求出![]() 点的坐标,并证明:
点的坐标,并证明:![]() 过圆心
过圆心![]() ;
;
(2)当![]() 时,求直线
时,求直线![]() 的方程.
的方程.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知|a|=4,|b|=8,a与b的夹角是120°.
(1) 计算:① |a+b|,② |4a-2b|;
(2) 当k为何值时,(a+2b)⊥(ka-b)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设l,m是两条不同的直线,α是一个平面,则下列命题正确的是( )
A. 若l⊥m,mα,则l⊥α
B. 若l⊥α,l∥m,则m⊥α
C. 若l∥α,mα,则l∥m
D. 若l∥α,m∥α,则l∥m
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在遂宁市中央商务区的街道,有一中年人吆喝“送钱”,只见他手拿一黑色小布袋,袋中有3只黄色、2只白色的乒乓球(其体积,质地完全相同),旁边立着一块小黑板写道:
摸球方法:从袋中随机摸出3个球,若摸得统一颜色的3个球,摊主送个摸球者10元钱;若摸得非同一颜色的3个球。摸球者付给摊主2元钱。
(1)摸出的3个球中至少有1个白球的概率是多少?
(2)假定一天中有100人次摸奖,试从概率的角度估算一下这个摊主一个月(按30天计)能赚多少钱?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设各项均为正数的数列![]() 的前n项和为
的前n项和为![]() ,满足
,满足![]() ,且
,且![]() ,公比大于1的等比数列
,公比大于1的等比数列![]() 满足
满足![]() ,
, ![]() .
.
(1)求证数列![]() 是等差数列,并求其通项公式;
是等差数列,并求其通项公式;
(2)若![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]() ;
;
(3)在(2)的条件下,若![]() 对一切正整数n恒成立,求实数t的取值范围.
对一切正整数n恒成立,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形![]() 为矩形,直线
为矩形,直线![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 在棱
在棱![]() 上.
上.
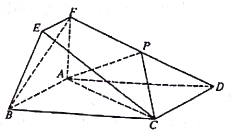
(1)求证:![]() ;
;
(2)若![]() 是
是![]() 的中点,求异面直线
的中点,求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(3)若![]()
![]()
![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com