
分析 (Ⅰ)函数f(x)关于(2,1)对称,即可求a的值,先将原函数变成f(x)=1+$\frac{3}{x-2}$,根据减函数的定义,设x1>x2>1,通过作差证明f(x1)<f(x2)即可.
(Ⅱ)g(x)=|x+1|+|2x-3|,即可画出函数g(x)的简图并求出该函数的值域.
解答 解:(Ⅰ)∵f(4-x)+f(x)=2,∴函数f(x)关于(2,1)对称,
∵f(x)=$\frac{ax+1}{x-2}$=a+$\frac{2a+1}{x-2}$,
∴a=1,
∴f(x)=1+$\frac{3}{x-2}$,
证明如下:
设x1>x2>3,则:f(x1)-f(x2)=$\frac{3({x}_{2}-{x}_{1})}{({x}_{1}-2)({x}_{2}-2)}$
∵x1>x2>3;
∴x2-x1<0,x1-2>0,x2-2>0;
∴f(x1)<f(x2);
∴f(x)在(3,+∞)上是单调减函数.
(Ⅱ)g(x)=|x+a|+|2x-3|=|x+1|+|2x-3|,
函数g(x)的简图如图所示,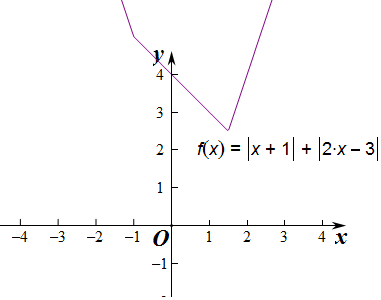
该函数的值域[2.5,+∞).
点评 考查分离常数法化简函数解析式,减函数的定义,以及根据减函数的定义证明一个函数为减函数的方法及过程.


 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{y-{y_1}}}{{x-{x_1}}}$=k表示过点P1(x1,y1),且斜率为k的直线方程 | |
| B. | 直线y=kx+b与 y 轴交于一点B(0,b),其中截距b=|OB| | |
| C. | 在x轴和y轴上的截距分别为a与b的直线方程是 $\frac{x}{a}$+$\frac{y}{b}$=1 | |
| D. | 方程(x2-x1)(y-y1)=(y2-y1)(x-x1)表示过点P1(x1,y1),P2(x2,y2)的直线 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
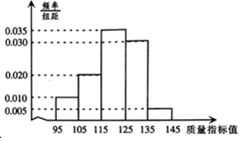 从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图,则这500件产品质量指标值的样本方差s2是110(同一组中的数据用该组区间的中点值作代表)
从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图,则这500件产品质量指标值的样本方差s2是110(同一组中的数据用该组区间的中点值作代表)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com