
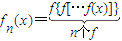 ,已知
,已知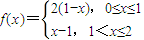 ,
,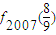 的值;
的值;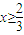 ,∴
,∴ .
.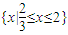 .
.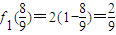 ,
, ,
,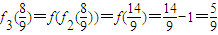 ,
,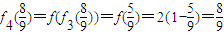 ,
, ,(k,r∈N*),
,(k,r∈N*),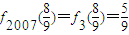 .
. 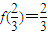 ,∴
,∴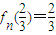 ,则
,则 ,
, .
.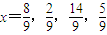 ,恒有f12(x)=f4×3(x)=x,
,恒有f12(x)=f4×3(x)=x,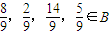 .
.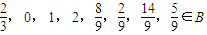 ,
,

科目:高中数学 来源: 题型:
| ||
| n个f |
|
| 8 |
| 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| n个f |
|
| 8 |
| 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| n个f |
|
|
|
| 8 |
| 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)
设n为正整数,规定:fn(x)=![]() ,已知f(x)= .
,已知f(x)= .
(1)解不等式f(x)≤x;
(2)设集合A={0,1,2},对任意x∈A,证明f3(x)=x;
(3)求f2007()的值;
(4)(理)若集合B=,证明B中至少包含8个元素.
查看答案和解析>>
科目:高中数学 来源:2010年上海市宝山区高三月考数学试卷2(文理合卷)(解析版) 题型:解答题
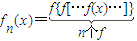 ,已知
,已知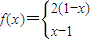
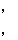
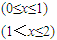 .
.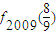 ;
;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com