
分析 (I)列出抽出的卡片的所有情况以及使|OP|=1的情况,利用古典概型解答;
(II)在[0,4]上先后取两个数分别记为x,y,为正方形区域,满足P点在第一象限的区域是满足$\left\{\begin{array}{l}0≤x≤4\\ 0≤y≤4\\ x-3>0\\ x-y>0\end{array}\right.$,分别求出面积,利用几何概型个数解答.
解答 解:(I)抽出的卡片的所有情况分别是:
| (x,y) | (2,2) | (2,3) | (2,4) | (3,2) | (3,3) | (3,4) | (4,2) | (4,3) | (4,4) |
| P坐标 | (-1,0) | (-1,-1) | (-1,-2) | (0,1) | (0,0) | (0,-1) | (1,2) | (1,1) | (1,0) |
| |OP| | 1 | $\sqrt{2}$ | $\sqrt{5}$ | 1 | 0 | 1 | $\sqrt{5}$ | $\sqrt{2}$ | 1 |
 …(10分)
…(10分)点评 本题考查了古典概型和几何概型的应用,古典概型关键是明确事件个数,几何概型关键是明确测度,利用长度、面积或者体积比求概率.


科目:高中数学 来源: 题型:选择题
| A. | 24$\sqrt{2}$ | B. | 8 | C. | 8$\sqrt{2}$ | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,侧面PAD是正三角形,底面ABCD直角梯形,AD∥BC,∠ADC=90°,AD=2BC=2,$CD=\sqrt{3}$,平面PAD⊥底面ABCD,若M为AD的中点.
如图,在四棱锥P-ABCD中,侧面PAD是正三角形,底面ABCD直角梯形,AD∥BC,∠ADC=90°,AD=2BC=2,$CD=\sqrt{3}$,平面PAD⊥底面ABCD,若M为AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=2为f(x)的极小值点 | B. | x=2为f(x)的极大值点 | ||
| C. | $x=\frac{1}{2}$为f(x)的极小值点 | D. | $x=\frac{1}{2}$为f(x)的极大值点 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3f(2ln2)<2f(2ln3) | B. | 3f(2ln2)>2f(2ln3) | C. | 2f(3ln3)<3f(2ln2) | D. | 2f(3ln3)>3f(2ln2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届山东潍坊临朐县高三10月月考数学(文)试卷(解析版) 题型:解答题
已知命题 指数函数
指数函数 单调递增;命题
单调递增;命题 ,
, .若命题“
.若命题“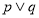 ”为真命题,命题“
”为真命题,命题“ ”为假命题,求实数
”为假命题,求实数 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com