|
|
|
已知集合M＝{－1，0，1}，N＝{0，1，2}，则M∪N＝
|
| [ ] |
A． |
{－1，0，1}
|
B． |
{－1，0，1，2}
|
C． |
{－1，0，2}
|
D． |
{0，1}
|
|
|
练习册系列答案
相关习题
科目：高中数学
来源：课标综合版 专题复习
题型：
|
|
|
如图，P是⊙O外一点，PA是切线，A为切点，割线PBC与⊙O相交于点B，C，PC＝2PA，D为PC的中点，AD的延长线交⊙O于点E，证明：
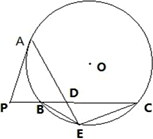
(Ⅰ)BE＝EC；
(Ⅱ)AD·DE＝2PB2．
|
|
|
查看答案和解析>>
科目：高中数学
来源：课标综合版 专题复习
题型：
|
|
|
直线l1和l2是圆x2＋y2＝2的两条切线，若l1与l2的交点为(1，3)，则l1与l2的夹角的正切值等于________．
|
|
|
查看答案和解析>>
科目：高中数学
来源：课标综合版 专题复习
题型：
|
|
|
对任意复数w1，w2，定义w1*w2＝w1 ，其中是w2的共轭复数，对任意复数z1，z2，z3，有如下四个命题：
①(z1＋z2)*z3＝(z1*z3)＋(z2*z3)
②z1*(z2＋z3)＝(z1*z2)＋(z1*z3)
③(z1*z2)*z3＝z1*(z2*z3)
④z1*z2＝z2*z1
则真命题的个数是
|
| [ ] |
A． |
1
|
B． |
2
|
C． |
3
|
D． |
4
|
|
|
查看答案和解析>>
科目：高中数学
来源：课标综合版 专题复习
题型：
|
|
|
某车间20名工人年龄数据如下表：
(1)求这20名工人年龄的众数与极差；
(2)以这十位数为茎，个位数为叶，作出这20名工人年龄的茎叶图；
(3)求这20名工人年龄的方差．
|
|
|
查看答案和解析>>
科目：高中数学
来源：课标综合版 专题复习
题型：
|
|
|
已知某地区中小学学生人数和近视情况分别如图1和如图2所示，为了解该地区中下学生的近视形成原因，用分层抽样的方法抽取2％的学生进行调查，则样本容量和抽取的高中生近视人数分别为
|
| [ ] |
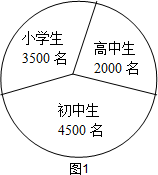
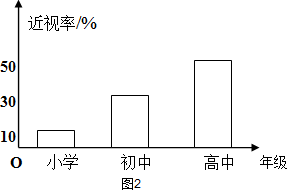
A． |
100，10
|
B． |
200，10
|
C． |
100，20
|
D． |
200，20
|
|
|
查看答案和解析>>
科目：高中数学
来源：课标综合版 专题复习
题型：
|
|
|
若等比数列{an}的各项均为正数，且a10a11＋a9a12＝2e5，则lna1＋lna2＋……＋lna20＝________．
|
|
|
查看答案和解析>>
科目：高中数学
来源：课标综合版 专题复习
题型：
|
|
|
要制作一个容积为4 m3，高为1 m的无盖长方体容器，已知该溶器的底面造价是每平方米20元，侧面造价是是每平方米10元，则该溶器的最低总造价是
|
| [ ] |
A． |
80元
|
B． |
120元
|
C． |
160元
|
D． |
240元
|
|
|
查看答案和解析>>
科目：高中数学
来源：课标综合版 专题复习
题型：
|
|
|
设a、b是实数，则“a＞b”是“a2＞b2”的
|
| [ ] |
A． |
充分而不必要条件
|
B． |
必要而不必要条件
|
C． |
充分必要条件
|
D． |
既不充分不必要条件
|
|
|
查看答案和解析>>
