
分析 对任意的x1,x2∈[$\frac{1}{2}$,2],都有f(x1)-g(x2)≥2成立等价于f(x)≥2+g(x)max.求得g(x)的最大值,进一步利用分离参数法,构造函数法,求得单调区间和最值,即可求得实数a的取值范围.
解答 解:对任意的x1,x2∈[$\frac{1}{2}$,2],都有f(x1)-g(x2)≥2成立
等价于f(x)≥2+g(x)max.
由g(x)=x3-x2-5的导数g′(x)=3x2-2x=x(3x-2),
在[$\frac{1}{2}$,$\frac{2}{3}$)上,g′(x)<0,g(x)递减;在($\frac{2}{3}$,2)上,g′(x)>0,g(x)递增.
g(2)=-1,g($\frac{1}{2}$)=-$\frac{41}{5}$,可得g(x)max=-1,
可得在[$\frac{1}{2}$,2]上,f(x)=$\frac{a}{x}$+xlnx≥1恒成立,等价于a≥x-x2lnx恒成立.
记h(x)=x-x2lnx,则h′(x)=1-2xlnx-x且h′(1)=0,
∴当$\frac{1}{2}$<x<1时,h′(x)>0;当1<x<2时,h′(x)<0,
∴函数h(x)在($\frac{1}{2}$,1)上单调递增,在(1,2)上单调递减,
∴h(x)max=h(1)=1.
∴a≥1.
故答案为:[1,+∞).
点评 本题考查了利用导数求闭区间上函数的最值,考查导数在研究函数问题中的应用、由不等式恒成立求解参数范围,考查了划归与转化的思想,属于中档题.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | x≥0? | B. | x≥1? | C. | x≥-1? | D. | x≥-3? |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
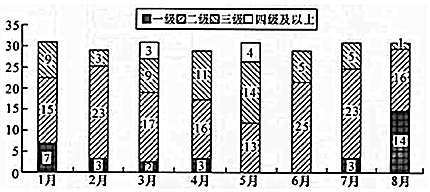
| A. | 1月至8月空气合格天数超过20天的月份有5个 | |
| B. | 第二季度与第一季度相比,空气达标天数的比重下降了 | |
| C. | 8月是空气质量最好的一个月 | |
| D. | 6月份的空气质量最差 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1} | B. | {-1,0,1,2,3} | C. | {1,2} | D. | {0,1,2,3} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com