练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    1．在平面直角坐标系xOy中，已知圆C1：（x-4）2+（y-8）2=1，圆C2：（x-6）2+（y+6）2=9．若圆心在x轴上的圆C同时平分圆C1和圆C2的圆周，则圆C的方程是x2+y2=81．

    分析 由题意，圆C与圆C1和圆C2的公共弦分别为圆C1和圆C2的直径，求出圆心坐标，可得结论．

    解答 解：由题意，圆C与圆C1和圆C2的公共弦分别为圆C1和圆C2的直径，
    设C（x，0），则（x-4）2+（0-8）2+1=（x-6）2+（0+6）2+9，∴x=0，
    ∴圆C的方程是x2+y2=81．
    故答案为x2+y2=81．

    点评 本题考查圆的方程，考查圆与圆的位置关系，考查学生的计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    11．2017年春晚分会场之一是凉山西昌，电视播出后，通过网络对凉山分会场的表演进行了调查．调查分三类人群进行，参加了网络调查的观众们的看法情况如下：
     观众对凉山分会场表演的看法 非常好 好
     中国人且非四川（人数比例） $\frac{1}{2}$ $\frac{1}{2}$
     四川人（非凉山）（人数比例）$\frac{2}{3}$  $\frac{1}{3}$
    凉山人（人数比例） $\frac{3}{4}$ $\frac{1}{4}$
    （1）从这三类人群中各选一个人，求恰好有2人认为“非常好”的概率（用比例作为相应概率）；
    （2）若在四川人（非凉山）群中按所持态度分层抽样，抽取9人，在这9人中任意选取3人，认为“非常好”的人数记为ξ，求ξ的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．已知集合M={1，3，4}，N={x|x2-4x+3=0}，则M∩N=（　　）
    A．{3，4}B．{1，4}C．{1，3}D．{3}

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．已知n=${∫}_{0}^{2}$x3dx，则（x-$\frac{1}{\root{3}{x}}$）n的展开式中常数项为-4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．已知复数z=$\frac{3-i}{1+i}$，其中i为虚数单位，则复数z的模是$\sqrt{5}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

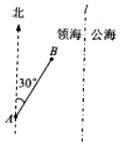    6．一缉私艇巡航至距领海边界线l（一条南北方向的直线）3.8海里的A处，发现在其北偏东30°方向相距4海里的B处有一走私船正欲逃跑，缉私艇立即追击，已知缉私艇的最大航速是走私船最大航速的3倍，假设缉私艇和走私船均按直线方向以最大航速航行．
    （1）若走私船沿正东方向逃离，试确定缉私艇的追击方向，使得用最短时间在领海内拦截成功；（参考数据：sin17°≈$\frac{\sqrt{3}}{6}$，$\sqrt{33}$≈5.7446）
    （2）问：无论走私船沿何方向逃跑，缉私艇是否总能在领海内成功拦截？并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．将函数y=cos（x-$\frac{π}{3}$）的图象上各点横坐标伸长到原来的2倍（纵坐标不变），再向左平移$\frac{π}{6}$个单位，所得函数图象的一条对称轴是（　　）
    A．x=$\frac{π}{4}$B．x=$\frac{π}{6}$C．x=πD．x=$\frac{π}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．已知函数f（x）=$\left\{\begin{array}{l}{{2}^{x}-4，x＞2}\\{\sqrt{-{x}^{2}+2x}，0≤x≤2}\end{array}\right.$若F（x）=f（x）-kx-3k在其定义域内有3个零点，则实数k的取值范围是（0，$\frac{\sqrt{15}}{15}$）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．已知函数 f（x）=$\frac{a}{x}$+xlnx，g（x）=x3-x2-5，若对任意的x1，x2∈[$\frac{1}{2}$，2]，都有f（x1）-g（x2）≥2成立，则a的取值范围是[1，+∞）．

    查看答案和解析>>

    同步练习册答案