
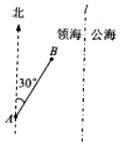
 一缉私艇巡航至距领海边界线l(一条南北方向的直线)3.8海里的A处,发现在其北偏东30°方向相距4海里的B处有一走私船正欲逃跑,缉私艇立即追击,已知缉私艇的最大航速是走私船最大航速的3倍,假设缉私艇和走私船均按直线方向以最大航速航行.
一缉私艇巡航至距领海边界线l(一条南北方向的直线)3.8海里的A处,发现在其北偏东30°方向相距4海里的B处有一走私船正欲逃跑,缉私艇立即追击,已知缉私艇的最大航速是走私船最大航速的3倍,假设缉私艇和走私船均按直线方向以最大航速航行.分析 (1)设缉私艇在C处与走私船相遇,则AC=3BC.△ABC中,由余弦定理、正弦定理即可求解;
(2)建立坐标系,求出P的轨迹方程,即可解决.
解答 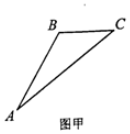 解:(1)设缉私艇在C处与走私船相遇,则AC=3BC.
解:(1)设缉私艇在C处与走私船相遇,则AC=3BC.
△ABC中,由正弦定理可得sin∠BAC=$\frac{sin120°}{3}$=$\frac{\sqrt{3}}{6}$,
∴∠BAC=17°,
∴缉私艇应向北偏东47°方向追击,
△ABC中,由余弦定理可得cos120°=$\frac{16+B{C}^{2}-A{C}^{2}}{8BC}$,∴BC≈1.68615.
B到边界线l的距离为3.8-4sin30°=1.8,
∵1.68615<1.8,
∴能最短时间在领海内拦截成功;
(2)以A为原点,建立如图所示的坐标系,则B(2,2$\sqrt{3}$),设缉私艇在P(x,y)出与走私船相遇,则PA=3PB,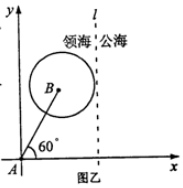
即x2+y2=9[(x-2)2+(y-2$\sqrt{3}$)2],即(x-$\frac{9}{4}$)2+(y-$\frac{9}{4}\sqrt{3}$)2=$\frac{9}{4}$,
∴P的轨迹是以($\frac{9}{4}$,$\frac{9}{4}\sqrt{3}$)为圆心,$\frac{3}{2}$为半径的圆,
∵圆心到边界线l:x=3.8的距离为1.55,大于圆的半径,
∴无论走私船沿何方向逃跑,缉私艇总能在领海内成功拦截.
点评 本题考查利用数学知识解决实际问题,考查正弦、余弦定理的运用,考查轨迹方程,属于中档题.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 8 | D. | $\frac{1}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+a,4 | B. | 1+a,4+a | C. | 1,4 | D. | 1,4+a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
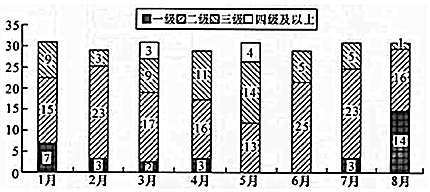
| A. | 1月至8月空气合格天数超过20天的月份有5个 | |
| B. | 第二季度与第一季度相比,空气达标天数的比重下降了 | |
| C. | 8月是空气质量最好的一个月 | |
| D. | 6月份的空气质量最差 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com