
分析 (1)求出函数的导数,计算x=1时y和y′的值,求出切线方程即可;
(2)令h(x)=g(x)+λf(x)=lnx+$\frac{λ}{{e}^{x}}$,(x>0),求出函数的导数,通过讨论λ的范围,求出函数的单调区间,从而证明结论即可;
(3)问题转化为$\frac{lnx}{{e}^{x}}$-a(x-1)≤0在(0,1]恒成立,令F(x)=$\frac{lnx}{{e}^{x}}$-a(x-1),根据函数的单调性求出a的范围.
解答 解:(1)y=f(x)g(x)=$\frac{lnx}{{e}^{x}}$,y′=$\frac{\frac{1}{x}-lnx}{{e}^{x}}$,
x=1时,y=0,y′=$\frac{1}{e}$,
故切线方程是:y=$\frac{1}{e}$x-$\frac{1}{e}$;
(2)证明:由g(x1)-g(x2)=λ[f(x2)-f(x1)],
得:g(x1)+λf(x1)=g(x2)+λf(x2),
令h(x)=g(x)+λf(x)=lnx+$\frac{λ}{{e}^{x}}$,(x>0),
h′(x)=$\frac{{e}^{x}-λx}{{xe}^{x}}$,
令ω(x)=ex-λx,则ω′(x)=ex-λ,
由x>0,得ex>1,
①λ≤1时,ω′(x)>0,ω(x)递增,
故h′(x)>0,h(x)递增,不成立;
②λ>1时,令ω′(x)=0,解得:x=lnλ,
故ω(x)在(0,lnλ)递减,在(lnλ,+∞)递增,
∴ω(x)≥ω(lnλ)=λ-λlnλ,
令m(λ)=λ-λlnλ,(λ>1),
则m′(λ)=-lnλ<0,故m(λ)递减,
又m(e)=0,
若λ≤e,则m(λ)≥0,ω(x)≥0,h(x)递增,不成立,
若λ>e,则m(λ)<0,函数h(x)有增有减,满足题意,
故λ>e;
(3)由f(x)g(x)≤a(x-1)得lnx-aex(x-1)≤0,
令F(x)=lnx-aex(x-1),x∈(0,1],
则F′(x)=$\frac{1}{x}$-axex=xex($\frac{1}{{x}^{2}{e}^{x}}$-a),F′(1)=$\frac{1}{e}$-a
①a≤$\frac{1}{e}$,因为$\frac{1}{{x}^{2}{e}^{x}}$≥$\frac{1}{e}$,xex>0,所以F′(x)≥0,
所以F(x)在(0,+∞]上为单调增函数,所以F(x)≤F(1)=0,故原不等式恒成立.
②法一:
当a>$\frac{1}{e}$,由(2)知ex≥ex,F′(x)≤$\frac{1}{x}$-aex2=$\frac{1-ae{x}^{3}}{x}$,
当(ae)${\;}^{-\frac{1}{3}}$<x<1时,F′(x)<0,F(x)为单调减函数.所以F(x)>F(1)=0,不合题意.
法二:
当a>$\frac{1}{e}$,一方面F′(1)=1-ae<0.
另一方面,?x1=$\frac{1}{ae}$<1,F(x1)≥$\frac{1}{{x}_{1}}$-aex1=x1($\frac{1}{{{x}_{1}}^{2}}$-ae)=x1ae(ae-1)>0.
所以?x1∈(x1,1),使F′(x0)=0,又,F′(x)在(0,+∞)上为单调减函数,
所以当x0<x<1时,使F′(x)<0,故F(x)在(x0,1)上为单调减函数.
所以F(x)>F(1)=0,不合题意.
综上:a≤$\frac{1}{e}$
点评 本题考查了切线方程问题,考查函数的单调性、最值问题,考查导数的应用以及分类讨论思想,考查不等式的证明,转化思想,是一道综合题.


 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | -2 | C. | $\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | -1 | C. | $\frac{5}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2,$\frac{5}{2}$] | B. | [$\frac{1}{2}$,$\frac{3}{2}$] | C. | (0,$\frac{1}{2}$] | D. | [$\frac{2}{5}$,$\frac{1}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 观众对凉山分会场表演的看法 | 非常好 | 好 |
| 中国人且非四川(人数比例) | $\frac{1}{2}$ | $\frac{1}{2}$ |
| 四川人(非凉山)(人数比例) | $\frac{2}{3}$ | $\frac{1}{3}$ |
| 凉山人(人数比例) | $\frac{3}{4}$ | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y2=4x | B. | y2=8x | C. | y2=3x | D. | y2=6x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$ | B. | $\frac{20}{3}$ | C. | 4 | D. | $\frac{16}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
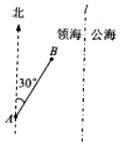 一缉私艇巡航至距领海边界线l(一条南北方向的直线)3.8海里的A处,发现在其北偏东30°方向相距4海里的B处有一走私船正欲逃跑,缉私艇立即追击,已知缉私艇的最大航速是走私船最大航速的3倍,假设缉私艇和走私船均按直线方向以最大航速航行.
一缉私艇巡航至距领海边界线l(一条南北方向的直线)3.8海里的A处,发现在其北偏东30°方向相距4海里的B处有一走私船正欲逃跑,缉私艇立即追击,已知缉私艇的最大航速是走私船最大航速的3倍,假设缉私艇和走私船均按直线方向以最大航速航行.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com