
分析 (Ⅰ)求出原函数的导函数,求得函数在点(1,f(1))处的切线l的方程,求得a,b值,进一步求出原函数的极小值点,得到f(x)的极小值;
(Ⅱ)把f(x)的解析式代入 $\frac{xf(x)}{4}$$+\frac{x}{{e}^{x}}$<$\frac{{x}^{4}}{6}$$+\frac{2}{e}$,转化为证 $\frac{x}{{e}^{x}}$-$\frac{2}{e}$<xlnx,分别构造函数g(x)=xlnx,x∈(0,+∞),h(x)=$\frac{x}{{e}^{x}}$-$\frac{2}{e}$ (0,+∞),然后利用导数分别求出它们的最值得到要证明的结论.
解答 解:(Ⅰ)f′(x)=ax2-$\frac{b}{x}$,
故f(1)=$\frac{1}{3}$a,f′(1)=a-b,
故切线方程是:y=(a-b)(x-1)+$\frac{1}{3}$a=(a-b)x-$\frac{2}{3}$a+b,
而y=-2x+$\frac{8}{3}$,故a-b=-2,-$\frac{2}{3}$a+b=$\frac{8}{3}$,
解得:a=2,b=4,
故f(x)=$\frac{2}{3}$x3-4lnx,(x>0),
f′(x)=2x2-$\frac{4}{x}$=$\frac{{2x}^{3}-4}{x}$(x>0),
当x∈(0,3$\sqrt{2}$)时,f′(x)<0;当x∈(3$\sqrt{2}$,+∞)时,f′(x)>0,
则f(x)在(0,3$\sqrt{2}$)上为减函数,在x(3$\sqrt{2}$,+∞)上为增函数,
∴f(x)的极小值为f(3$\sqrt{2}$)=$\frac{4}{3}$-4ln$\root{3}{2}$=$\frac{4}{3}$(1-ln2),无极大值;
(2)证明:f(x)=$\frac{2}{3}$x3-4lnx,
要证 $\frac{xf(x)}{4}$$+\frac{x}{{e}^{x}}$<$\frac{{x}^{4}}{6}$$+\frac{2}{e}$,即证 $\frac{x}{{e}^{x}}$-$\frac{2}{e}$<xlnx.
令g(x)=xlnx,x∈(0,+∞),
则g′(x)=lnx+1,
由g′(x)<0,得0<x<$\frac{1}{e}$;由g′(x)>0,得x>$\frac{1}{e}$,
∴当x=$\frac{1}{e}$时取得最小值,最小值为g($\frac{1}{e}$)=-$\frac{1}{e}$,
由h(x)=$\frac{x}{{e}^{x}}$-$\frac{2}{e}$,可得h′(x)=$\frac{1-x}{{e}^{x}}$,
∴当x∈(0,1),h′(x)>0,h(x)单调递增,
当x∈(1,+∞),h′(x)<0,h(x)单调递减.
函数h(x)(x>0)在x=1时取得最大值,
又h(1)=-$\frac{1}{e}$,∴h(x)<-$\frac{1}{e}$,
∴任意x∈(0,+∞),$\frac{xf(x)}{4}$$+\frac{x}{{e}^{x}}$<$\frac{{x}^{4}}{6}$$+\frac{2}{e}$.
点评 本题考查利用导数研究过曲线上某点处的切线方程,考查函数极值的求法,考查了数学转化思想方法,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | [2,$\frac{5}{2}$] | B. | [$\frac{1}{2}$,$\frac{3}{2}$] | C. | (0,$\frac{1}{2}$] | D. | [$\frac{2}{5}$,$\frac{1}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
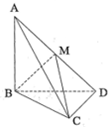 如图,三棱锥A-BCD中,AB⊥平面BCD,CD⊥BD.
如图,三棱锥A-BCD中,AB⊥平面BCD,CD⊥BD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
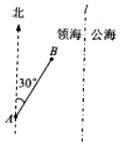 一缉私艇巡航至距领海边界线l(一条南北方向的直线)3.8海里的A处,发现在其北偏东30°方向相距4海里的B处有一走私船正欲逃跑,缉私艇立即追击,已知缉私艇的最大航速是走私船最大航速的3倍,假设缉私艇和走私船均按直线方向以最大航速航行.
一缉私艇巡航至距领海边界线l(一条南北方向的直线)3.8海里的A处,发现在其北偏东30°方向相距4海里的B处有一走私船正欲逃跑,缉私艇立即追击,已知缉私艇的最大航速是走私船最大航速的3倍,假设缉私艇和走私船均按直线方向以最大航速航行.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com