练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    11．设f（x）是定义在R上的奇函数，当x≤0时，f（x）=2x2-x，则f（1）=（　　）
    A．1B．3C．-3D．0

    分析 由奇函数性质得当x＞0时，f（x）=-2x2-x，由此能求出f（1）．

    解答 解：∵f（x）是定义在R上的奇函数，
    当x≤0时，f（x）=2x2-x，
    ∴当x＞0时，f（x）=-2x2-x，
    ∴f（1）=-2-1=-3．
    故选：C．

    点评 本题考查函数值的求法，是基础题，解题时要认真审题，注意函数性质的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    1．抛物线y2=2px（p＞0）的焦点为F，过焦点F且倾斜角为$\frac{π}{3}$的直线与抛物线相交于A，B两点，若|AB|=8，则抛物线的方程为（　　）
    A．y2=4xB．y2=8xC．y2=3xD．y2=6x

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

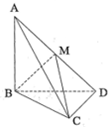    2．如图，三棱锥A-BCD中，AB⊥平面BCD，CD⊥BD．
    （1）求证：CD⊥平面ABD；
    （2）若AB=BD=CD=2，M为AD中点，求点A到平面MBC的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．函数f（x）=$\sqrt{lg（5-{x}^{2}）}$的定义域是[-2，2]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

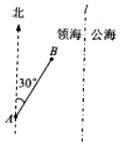    6．一缉私艇巡航至距领海边界线l（一条南北方向的直线）3.8海里的A处，发现在其北偏东30°方向相距4海里的B处有一走私船正欲逃跑，缉私艇立即追击，已知缉私艇的最大航速是走私船最大航速的3倍，假设缉私艇和走私船均按直线方向以最大航速航行．
    （1）若走私船沿正东方向逃离，试确定缉私艇的追击方向，使得用最短时间在领海内拦截成功；（参考数据：sin17°≈$\frac{\sqrt{3}}{6}$，$\sqrt{33}$≈5.7446）
    （2）问：无论走私船沿何方向逃跑，缉私艇是否总能在领海内成功拦截？并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．已知向量$\overrightarrow a，\overrightarrow b$满足$|{\overrightarrow a}|=|{\overrightarrow b}|=2$，$\overrightarrow a$与$\overrightarrow b$的夹角为60°，则$\overrightarrow b$在$\overrightarrow a$方向上的投影是1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．在△ABC中，角A，B，C的对边分别为a，b，c，且$\frac{cosB}{b}$=-$\frac{3cosC}{c}$，则角A的最大值是（　　）
    A．$\frac{π}{6}$B．$\frac{π}{4}$C．$\frac{π}{3}$D．$\frac{π}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

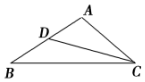    3．如图所示，给出下列条件：
    ①∠B=∠ACD；
    ②∠ADC=∠ACB；
    ③$\frac{AC}{CD}$=$\frac{AB}{BC}$；
    ④AC2=AD•AB．
    其中能够单独判定△ABC∽△ACD的个数为（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

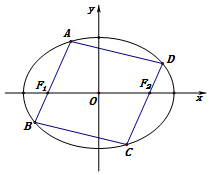    4．已知椭圆E的方程是$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1，左、右焦点分别是F1、F2，在椭圆E上有一动点A，过A、F1作一个平行四边形，使顶点A、B、C、D都在椭圆E上，如图所示．
    （Ⅰ） 判断四边形ABCD能否为菱形，并说明理由．
    （Ⅱ） 当四边形ABCD的面积取到最大值时，判断四边形ABCD的形状，并求出其最大值．

    查看答案和解析>>

    同步练习册答案