Question

1．将两封信投入3个编号为1，2，3的信箱，用X，Y分别表示投入第1，2号信箱的信的数目，求（X，Y）的边缘分布律，并判断X与Y是否独立．

Answer 1

分析 首先确定（X，Y）的所有可能取值，并用古典概型求出相应值的概率，即可求出（X，Y）的联合分布律，由此能求出结果．

解答 解：将两封信投到三个箱的投法有n=3²=9，X和Y的可能取值均为0，1，2，
P（X=0，y=0）=P（两封信都投入第3号信箱）=$\frac{1}{9}$，
P（X=1，Y=0）=P（两封信中一封投入第1号信箱，另一封投入第3号信箱）=$\frac{{C}_{2}^{1}{C}_{1}^{1}}{9}$=$\frac{2}{9}$，
同理，得：P（X=0，Y=1）=$\frac{2}{9}$，
P（X=1，Y=1）=$\frac{2}{9}$，
P（X=1，Y=2）=P（X=2，Y=1）=P（X=2，Y=2）=0，
从而得到（X，Y）的联合分布律，
P（X=k）=$\sum_{i=0}^{2}P（X=k，Y=i），k=0，1，2$，P（X=K）=$\sum_{i=0}^{2}P（X=i，Y=k）$，k=0，1，2，
∴（X，Y）的边缘分布律为：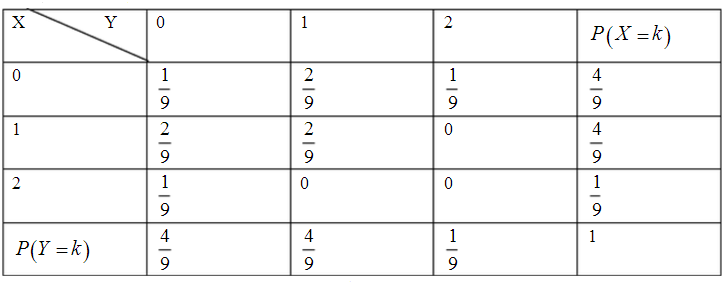
 
X的边缘分布律在表中的最后一列，Y的边缘分布很在表中的最后一行，
∵P（X=0，Y=0）=$\frac{1}{9}$，P（X=0）P（Y=0）=$\frac{4}{9}×\frac{4}{9}=\frac{16}{81}$≠$\frac{1}{9}$，
∴X与Y不独立．

点评 二维离散型随机变量的联合分列很，在实际问题中可利用事件的科积（交）的概率求得，此时概率的简洁公式是十分常用的计算技巧．