
某校为了探索一种新的教学模式,进行了一项课题实验,甲班为实验班,乙班为对比班,甲乙两班的人数均为50人,一年后对两班进行测试,测试成绩的分组区间为[80,90)、[90,100)、[100,110)、[110,120)、[120,130),由此得到两个班测试成绩的频率分布直方图:
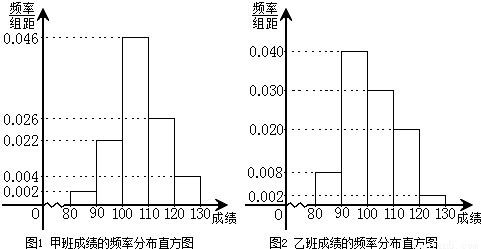
(Ⅰ)完成下面2×2列联表,你能有97.5%的把握认为“这两个班在这次测试中成绩的差异与实施课题实验有关”吗?并说明理由;
| 成绩小于100分 | 成绩不小于100分 | 合计 |
甲班 | a= _________ | b= _________ | 50 |
乙班 | c=24 | d=26 | 50 |
合计 | e= _________ | f= _________ | 100 |
(Ⅱ)现从乙班50人中任意抽取3人,记ξ表示抽到测试成绩在[100,120)的人数,求ξ的分布列和数学期望Eξ.
附:K2=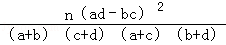 ,其中n=a+b+c+d
,其中n=a+b+c+d
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.204 | 6.635 | 7.879 | 10.828 |
(Ⅰ)有97.5%的把握认为这两个班在这次测试中成绩的差异与实施课题实验有关;
(Ⅱ)分布列见解析, .
.
【解析】
试题分析:
解题思路:(Ⅰ)补充完整 列联表,利用
列联表,利用 公式求值,结合临界值表进行判断;(Ⅱ)利用超几何分布的概率公式求各自概率值,列表格得出分布列,再套用公式求期望.
公式求值,结合临界值表进行判断;(Ⅱ)利用超几何分布的概率公式求各自概率值,列表格得出分布列,再套用公式求期望.
规律总结:求随机变量的分布列、期望、方差的一般步骤:①列出随机变量的所有可能取值;②求各个取值的概率(往往利用古典概型、几何概型、超几何分布、两点分布、二项分布等概率模型);③列出表格,即得随机变量的分布列;④根据期望定义求期望;⑤根据方差定义求方差(注意:求两点分布、二项分布的期望与方差时,要注意利用公式求解).
试题解析:(Ⅰ)由题意求得: ,
, ,
,

 有97.5%的把握认为这两个班在这次测试中成绩的差异与实施课题实验有关
有97.5%的把握认为这两个班在这次测试中成绩的差异与实施课题实验有关
(Ⅱ)乙班测试成绩在[100,120)的有25人, 可取0,1,2,3,
可取0,1,2,3,


 的分布列是
的分布列是
| 0 | 1 | 2 | 3 |
|
|
|
|
|
 .
.
考点:1.独立性检验的基本思想;2.随机变量的分布列;3.随机变量的期望.


 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源:2015届山东省高二暑假作业二数学试卷(解析版) 题型:选择题
点 到图形
到图形 上每一个点的距离的最小值称为点
上每一个点的距离的最小值称为点 到图形
到图形 的距离,那么平面内到定圆
的距离,那么平面内到定圆 的距离与到定点
的距离与到定点 的距离相等的点的轨迹不可能是( )
的距离相等的点的轨迹不可能是( )
A.圆 B.椭圆 C.双曲线的一支 D.直线
查看答案和解析>>
科目:高中数学 来源:2015届山东省菏泽市高二下学期期末考试理科数学试卷(解析版) 题型:解答题
(Ⅰ)已知复数z=1﹣i(i是虚数单位),若z2+a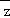 +b=3﹣3i,求实数a,b的值.
+b=3﹣3i,求实数a,b的值.
(Ⅱ)求二项式( +
+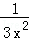 )10展开式中的常数项.
)10展开式中的常数项.
查看答案和解析>>
科目:高中数学 来源:2015届山东省菏泽市高二下学期期末考试理科数学试卷(解析版) 题型:选择题
某班有60名学生,一次考试后数学成绩ξ~N(110,102),若P(100≤ξ≤110)=0.35,则估计该班学生数学成绩在120分以上的人数为( ).
A.10 B.9 C.8 D.7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com