
已知抛物线 过点
过点 .
.
(1)求抛物线 的方程,并求其准线方程;
的方程,并求其准线方程;
(2)过焦点 且斜率为
且斜率为 的直线
的直线 与抛物线交于
与抛物线交于 两点,求
两点,求 的面积.
的面积.
(1)抛物线的方程为 ,准线方程为
,准线方程为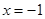 ;(2)
;(2)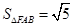 .
.
解析试题分析:(1)先由抛物线 过点
过点 得到
得到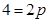 ,进而解出
,进而解出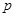 的值,这样即可确定该抛物线的方程,进而再根据抛物线的几何性质得到准线方程
的值,这样即可确定该抛物线的方程,进而再根据抛物线的几何性质得到准线方程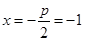 ;(2)由(1)中抛物线的方程先确定
;(2)由(1)中抛物线的方程先确定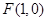 ,进而根据点斜式可写出直线
,进而根据点斜式可写出直线 的方程
的方程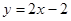 ,设点
,设点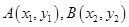 ,联立直线与抛物线的方程,消去
,联立直线与抛物线的方程,消去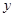 得到
得到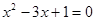 ,进而根据二次方程根与系数的关系得到
,进而根据二次方程根与系数的关系得到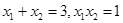 ,进而可根据弦长计算公式
,进而可根据弦长计算公式 计算出弦长
计算出弦长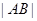 ,然后由点到直线的距离公式算出原点
,然后由点到直线的距离公式算出原点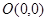 到直线
到直线 的距离
的距离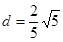 ,进而可求出
,进而可求出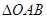 的面积.
的面积.
(1)根据抛物线 过点
过点 可得
可得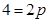 ,解得
,解得
从而抛物线的方程为 ,准线方程为
,准线方程为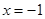 5分
5分
(2)抛物线焦点坐标为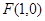 ,所以直线
,所以直线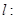
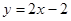 6分
6分
设点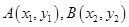
联立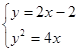 得:
得: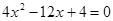 ,即
,即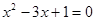 8分
8分
则由韦达定理有: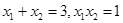 9分
9分
则弦长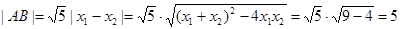 11分
11分
而原点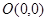 到直线
到直线 的距离
的距离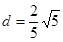 12分
12分
故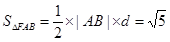 13分.
13分.
考点:1.抛物线的标准方程及其几何性质;2.直线与抛物线的位置关系;3.点到直线的距离公式.


科目:高中数学 来源: 题型:填空题
(2013·天津高考)已知抛物线y2=8x的准线过双曲线 -
- =1(a>0,b>0)的一个焦点,且双曲线的离心率为2,则该双曲线的方程为____________.
=1(a>0,b>0)的一个焦点,且双曲线的离心率为2,则该双曲线的方程为____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com