
 的△ABC的个数为2;
的△ABC的个数为2; 的夹角为钝角,则实数λ的取值范围为
的夹角为钝角,则实数λ的取值范围为 ;
; ;
;  ;
;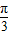 而y=sinx+cosx=
而y=sinx+cosx= sin(x+
sin(x+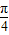 ),结合已知所求的x的范围可求y的范围.
),结合已知所求的x的范围可求y的范围.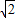 ,A=45°,
,A=45°,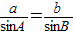 即
即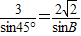 ,∴sinB=
,∴sinB= ,∵a>b,∴A>B,则B有1解,
,∵a>b,∴A>B,则B有1解, •
•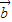 =(-2,1)•(λ,-1)=-2λ-1<0,得λ>-
=(-2,1)•(λ,-1)=-2λ-1<0,得λ>- ,若为反向向量,则λ=2
,若为反向向量,则λ=2 ,且λ≠2,即λ∈(-
,且λ≠2,即λ∈(- ,2)∪(2,+∞)
,2)∪(2,+∞) ,2)∪(2,+∞).故③为假命题;
,2)∪(2,+∞).故③为假命题;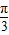 ,y=sinx+cosx=
,y=sinx+cosx=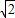 sin(x+
sin(x+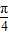 )
)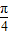 <
<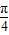 +x≤
+x≤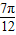 ,
,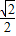 <sin(x+
<sin(x+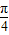 )≤1
)≤1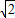 .故④为真命题;
.故④为真命题;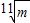 -1,故⑤为真命题;
-1,故⑤为真命题;

科目:高中数学 来源: 题型:
| 2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x |
| x2+1 |
| 3 |
| 4 |
| 1 |
| 3 |
| 3 |
| 10 |
| 3 |
| 4 |
| a |
| a2+1 |
| b |
| b2+1 |
| c |
| c2+1 |
| 9 |
| 10 |
| n |
 |
| k=1 |
| ak | ||
|
查看答案和解析>>
科目:高中数学 来源:2014届山东省日照市高三上学期第一次月考理科数学试卷(解析版) 题型:填空题
下列结论中是真命题的是__________(填序号).
①f(x)=ax2+bx+c在[0,+∞)上是增函数的一个充分条件是- <0;
<0;
②已知甲:x+y≠3,乙:x≠1或y≠2,则甲是乙的充分不必要条件;
③数列{an}(n∈N*)是等差数列的充要条件是Pn 是共线的.
是共线的.
查看答案和解析>>
科目:高中数学 来源:2014届福建省高二下学期期中考试理科数学试卷(解析版) 题型:填空题
给出下列四个结论:① 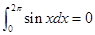 ;
;
②已知集合 ,若
,若 ,则
,则 1
1
③已知 为定义在R上的可导函数,且
为定义在R上的可导函数,且 对于
对于 恒成立,则有
恒成立,则有 ,
,  ;
;
④ 若定义在正整数有序对集合上的二元函数 满足:(1)
满足:(1) ,(2)
,(2) (3)
(3) ,则
,则 =
=
则其中正确结论的有 (填写你认为正确的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
下列结论中是真命题的是__________(填序号).
①f(x)=ax2+bx+c在[0,+∞)上是增函数的一个充分条件是-![]() <0;
<0;
②已知甲:x+y≠3,乙:x≠1或y≠2,则甲是乙的充分不必要条件;
③数列{an}(n∈N*)是等差数列的充要条件是Pn![]() 是共线的.
是共线的.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com