Question

2．函数f（x）=lnx在点P（x₀，f（x₀））处的切线l与函数lg（x）=e^x的图象也相切，则满足条件的切点P的个数有（　　）

• A． 0个
• B． 1个
• C． 2个
• D． 3个

Answer 1

分析 先求直线l为函数的图象上一点A（x₀，f （x₀））处的切线方程，再设直线l与曲线y=g（x）相切于点（x₁，e${\;}^{{x}_{1}}$），进而可得lnx₀=$\frac{{x}_{0}+1}{{x}_{0}-1}$，即可得出结论．

解答 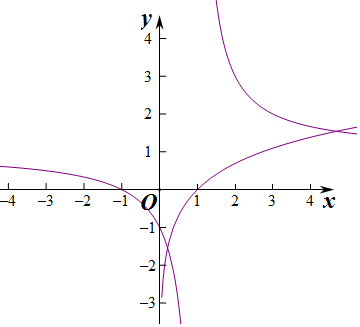解：∵f（x）=lnx，
∴f′（x）=$\frac{1}{x}$，
∴x=x₀，f′（x₀）=$\frac{1}{{x}_{0}}$，
∴切线l的方程为y-lnx₀=$\frac{1}{{x}_{0}}$（x-x₀），
即y=$\frac{1}{{x}_{0}}$x+lnx₀-1，①
设直线l与曲线y=g（x）
相切于点（x₁，e${\;}^{{x}_{1}}$），
∵g'（x）=e^x，∴e${\;}^{{x}_{1}}$=$\frac{1}{{x}_{0}}$，
∴x₁=-lnx₀．
∴直线l也为y-$\frac{1}{{x}_{0}}$=$\frac{1}{{x}_{0}}$（x+lnx₀），
即y=$\frac{1}{{x}_{0}}$x+$\frac{ln{x}_{0}}{{x}_{0}}$+$\frac{1}{{x}_{0}}$，②
由①②得lnx₀=$\frac{{x}_{0}+1}{{x}_{0}-1}$，
作出y=lnx和y=$\frac{x+1}{x-1}$的图象，
如图所示，图象有两个交点，方程有两解．
故选：C．

点评 本题以函数为载体，考查导数知识的运用，考查曲线的切线，同时考查零点存在性定理，综合性比较强．