
已知定点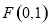 和直线
和直线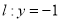 ,过点
,过点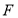 且与直线
且与直线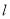 相切的动圆圆心为点
相切的动圆圆心为点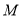 ,记点
,记点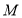 的轨迹为曲线
的轨迹为曲线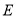 .
.
(1)求曲线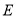 的方程;
的方程;
(2)若点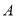 的坐标为
的坐标为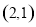 ,直线
,直线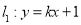 (
(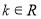 ,且
,且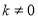 )与抛物线
)与抛物线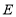 ,相交于
,相交于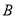 、
、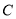 两点,直线
两点,直线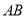 、
、 分别交直线
分别交直线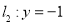 于点
于点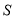 、
、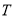 试判断以线段
试判断以线段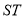 为直径的圆是否恒过两个定点?若是,求这两个定点的坐标;若不是,说明理由.
为直径的圆是否恒过两个定点?若是,求这两个定点的坐标;若不是,说明理由.
(1)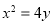 ;(2)存在,且两个定点坐标为
;(2)存在,且两个定点坐标为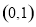 和
和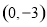 .
.
【解析】
试题分析:(1)解法1是根据题干条件确定曲线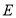 是以点
是以点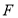 为焦点、以直线
为焦点、以直线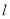 为准线的抛物线,从而写出抛物线
为准线的抛物线,从而写出抛物线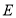 的方程;解法2是利用直接法求动点
的方程;解法2是利用直接法求动点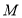 的轨迹方程,即设点
的轨迹方程,即设点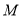 的坐标为
的坐标为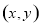 ,将条件转化为点
,将条件转化为点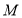 到点
到点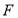 的距离等于点到直线
的距离等于点到直线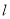 的距离相等列等式,化简后即得到曲线
的距离相等列等式,化简后即得到曲线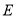 的方程;(2)解法1是先设点
的方程;(2)解法1是先设点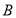 、
、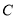 的坐标分别为
的坐标分别为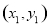 、
、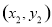 ,将直线
,将直线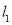 的方程与抛物线
的方程与抛物线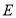 的方程联立求出
的方程联立求出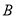 、
、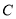 的坐标,并求出
的坐标,并求出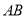 、
、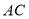 的直线方程,与直线
的直线方程,与直线 的方程联立求出
的方程联立求出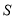 、
、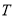 的坐标,利用两点间的距离公式求出
的坐标,利用两点间的距离公式求出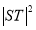 ,然后求出线段
,然后求出线段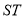 的中点的坐标,然后写出以
的中点的坐标,然后写出以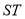 为直径的圆的方程,结合韦达定理进行化简,根据方程的结构特点求出定点的坐标;解法2是设直线
为直径的圆的方程,结合韦达定理进行化简,根据方程的结构特点求出定点的坐标;解法2是设直线 的方程为
的方程为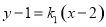 ,点
,点 的坐标为
的坐标为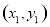 ,分别将直线
,分别将直线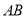 的方程与抛物线和直线
的方程与抛物线和直线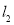 的方程求出点
的方程求出点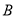 、
、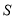 的坐标,然后设直线
的坐标,然后设直线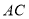 的方程为
的方程为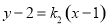 ,利用同样的方法求出点
,利用同样的方法求出点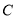 、
、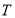 的坐标,利用点
的坐标,利用点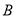 、
、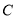 都在直线
都在直线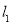 上,结合两点连线的斜率等于
上,结合两点连线的斜率等于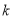 值以及点
值以及点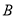 在直线
在直线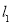 得到
得到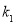 、
、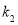 与
与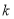 之间的等量关系(韦达定理),然后设
之间的等量关系(韦达定理),然后设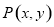 为以
为以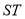 为直径的圆上的一点,由
为直径的圆上的一点,由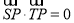 得到以
得到以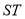 为直径的圆的方程,然后圆的方程的结构特点求出定点的坐标.
为直径的圆的方程,然后圆的方程的结构特点求出定点的坐标.
试题解析:(1)解法1:由题意,点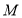 到点
到点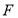 的距离等于它到直线
的距离等于它到直线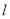 的距离,
的距离,
故点 的轨迹是以点
的轨迹是以点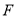 为焦点,
为焦点,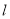 为准线的抛物线.
为准线的抛物线.
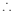 曲线
曲线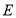 的方程为
的方程为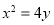 ;
;
解法2:设点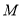 的坐标为
的坐标为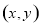 ,依题意,得
,依题意,得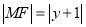 ,即
,即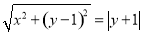 ,
,
化简得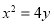 .
.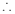 曲线
曲线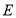 的方程为
的方程为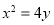 ;
;
解法1:(2)设点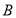 、
、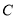 的坐标分别为
的坐标分别为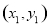 、
、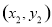 ,依题意,
,依题意,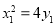 ,
,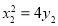 ,
,
由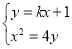 消去
消去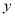 得
得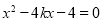 ,解得
,解得 .
.
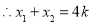 ,
,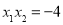 ,
,
直线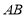 的斜率
的斜率 ,故直线
,故直线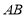 的方程为
的方程为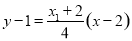 .
.
令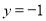 ,得
,得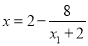 ,
,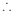 点
点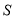 的坐标为
的坐标为 .
.
同理可得点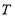 的坐标为
的坐标为 .
.
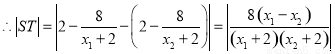
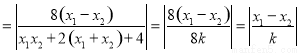 .
.
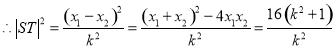 ,
,
设线段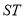 的中点坐标为
的中点坐标为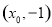 ,则
,则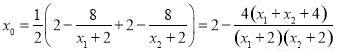
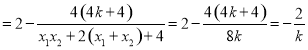 .
.
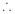 以线段
以线段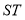 为直径的圆的方程为
为直径的圆的方程为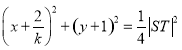
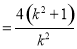 .
.
展开得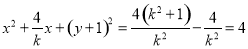 .令
.令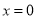 ,得
,得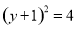 ,解得
,解得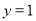 或
或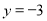 .
.
 以线段
以线段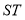 为直径的圆恒过两个定点
为直径的圆恒过两个定点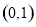 、
、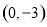 ;
;
解法2:由(1)得抛物线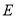 的方程为
的方程为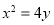 .
.
设直线 的方程为
的方程为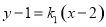 ,点
,点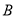 的坐标为
的坐标为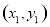 ,
,
由 ,解得
,解得 ,
,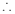 点
点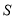 的坐标为
的坐标为 .
.
由 ,消去
,消去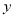 ,得
,得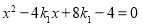 ,
,
即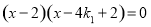 ,解得
,解得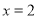 或
或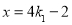 .
.
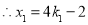 ,
,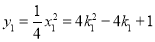 .
.
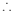 点
点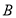 的坐标为
的坐标为 .
.
同理,设直线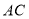 的方程为
的方程为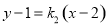 ,
,
则点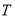 的坐标为
的坐标为 ,点
,点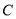 的坐标为
的坐标为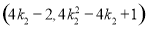 .
.
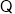 点
点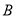 、
、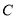 在直线
在直线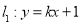 上,
上,
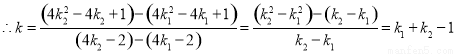 .
.
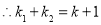 .
.
又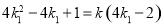
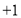 ,得
,得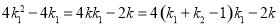 ,
,
化简得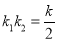 .
.
设点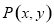 是以线段
是以线段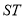 为直径的圆上任意一点,则
为直径的圆上任意一点,则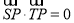 ,
,
得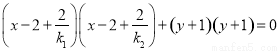 ,
,
整理得,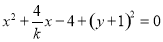 .
.
令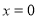 ,得
,得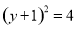 ,解得
,解得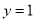 或
或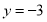 .
.
 以线段
以线段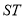 为直径的圆恒过两个定点
为直径的圆恒过两个定点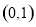 、
、 .
.
考点:1.抛物线的定义与方程;2.动点的轨迹方程;3.距离公式;4.直线与抛物线的位置关系;5.韦达定理


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源:2013-2014学年广东省揭阳市高三4月第二次模拟考试文科数学试卷(解析版) 题型:选择题
已知命题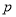 :函数
:函数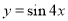 是最小正周期为
是最小正周期为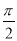 的周期函数,命题
的周期函数,命题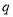 :函数
:函数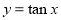 在
在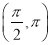 上单调递减,则下列命题为真命题的是( )
上单调递减,则下列命题为真命题的是( )
A.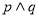 B.
B.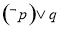
C.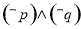 D.
D.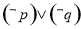
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省广州市毕业班综合测试二理科数学试卷(解析版) 题型:填空题
在平行四边形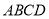 中,点
中,点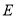 在线段
在线段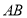 上,且
上,且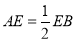 ,连接
,连接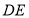 ,若
,若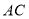 与
与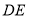 相交于点
相交于点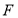 ,
,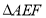 的面积为
的面积为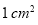 ,则
,则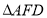 的面积为
的面积为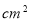 .
.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省广州市毕业班综合测试二理科数学试卷(解析版) 题型:选择题
将正偶数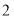 、
、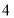 、
、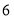 、
、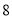 、
、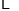 按表
按表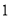 的方式进行排列,记
的方式进行排列,记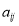 表示第
表示第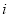 行和第
行和第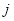 列的数,若
列的数,若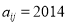 ,则
,则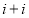 的值为( )
的值为( )
| 第 | 第 | 第 | 第 | 第 |
第 |
|
|
|
|
|
第 |
|
|
|
|
|
第 |
|
|
|
|
|
第 |
|
|
|
|
|
第 |
|
|
|
|
|
|
|
|
|
|
|
A.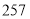 B.
B.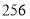 C.
C.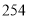 D.
D.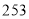
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com