
���� ��������Բ��������e=$\frac{c}{a}$=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$=$\frac{1}{2}$����a2=2b2������������OAB�����ȣ�$\frac{1}{2}$ab=$\frac{1}{2}$��$\frac{2\sqrt{21}}{7}$•$\sqrt{{a}^{2}+{b}^{2}}$�����뼴�����a��b��ֵ�������Բ���̣�
����ֱ�߷��̴�����Բ���̣��ɡ�=0��4k2-n2+3=0����F1P��l��F2Q��l��ֱ������F1PQF2��λ�߳�d1=$\frac{حnح}{\sqrt{1+{k}^{2}}}$����F2��1��0��ֱ��F1P�ľ���d2=$\frac{2}{\sqrt{1+{k}^{2}}}$��${S}_{{F}_{1}PQ{F}_{2}}$=d1•d2=$\frac{2حnح}{1+{k}^{2}}$=2$\sqrt{\frac{4{k}^{2}+3}{��1+{k}^{2}��^{2}}}$������ݺ����ĵ����ԣ���������ı���F1PQF2���S��ȡֵ��Χ��
��� �⣺�����������֪����ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0��������x���ϣ�
��Բ��������e=$\frac{c}{a}$=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$=$\frac{1}{2}$����a2=2b2��
������ϵԭ��O��ֱ��AB�ľ���Ϊ$\frac{2\sqrt{21}}{7}$��
��$\frac{1}{2}$ab=$\frac{1}{2}$��$\frac{2\sqrt{21}}{7}$•$\sqrt{{a}^{2}+{b}^{2}}$��
��$\frac{\sqrt{3}}{2}$a2=$\frac{2\sqrt{21}}{7}$$\sqrt{{a}^{2}+\frac{3}{4}{a}^{2}}$��
��ã�a=2��b=$\sqrt{3}$��
����ԲC�ķ���Ϊ��$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$��
������ֱ��l����Բ����һ�������㣬
��$\left\{\begin{array}{l}{y=kx+n}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$���������3+4k2��x2+8knx=4n2-12=0��
�ɡ�=0��4k2-n2+3=0��
��F1P��l��F2Q��l��
����k��0����ֱ������F1PQF2��λ�߳�d1=$\frac{حnح}{\sqrt{1+{k}^{2}}}$��
ֱ��F1P�ķ���Ϊ��x+ky+1=0��
��F2��1��0��ֱ��F1P�ľ���d2=$\frac{2}{\sqrt{1+{k}^{2}}}$��
${S}_{{F}_{1}PQ{F}_{2}}$=d1•d2=$\frac{2حnح}{1+{k}^{2}}$=2$\sqrt{\frac{4{k}^{2}+3}{��1+{k}^{2}��^{2}}}$��
��t=3+4k2��
��S=8$\frac{t}{2{t}^{2}+2t+1}$=8$\sqrt{\frac{1}{t+\frac{1}{t}+2}}$��
��t��3����˫������֪S��t��3�ϵ����ݼ���
��0��S��2$\sqrt{3}$��
�ڵ�k=0ʱ��n=��$\sqrt{3}$��S=2$\sqrt{3}$��
�����������ı���F1PQF2���Sȡֵ��ΧΪ��0��2$\sqrt{3}$]��
���� ���⿼����Բ�����̣�ֱ������Բ��λ�ù�ϵ������㵽ֱ�ߵľ��빫ʽ��˫�������ĵ����Ե�Ӧ�ã�������������������е��⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{10}$ | B�� | 2$\sqrt{3}$ | C�� | 2$\sqrt{5}$ | D�� | $\sqrt{21}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��1 | B�� | a��1��a��$\frac{2}{��}$ | C�� | a��1��a��0 | D�� | a$��\frac{2}{��}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��0��2�� | B�� | ��-1��2] | C�� | ��0��2] | D�� | ��-1��3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
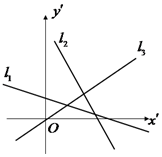 ��ͼ����ƽ��ֱ������ϵ��������ֱ��l1��l2��l3�����Ӧ��б�ʷֱ�Ϊk1��k2��k3��������ѡ������ȷ���ǣ�������
��ͼ����ƽ��ֱ������ϵ��������ֱ��l1��l2��l3�����Ӧ��б�ʷֱ�Ϊk1��k2��k3��������ѡ������ȷ���ǣ�������| A�� | k3��k1��k2 | B�� | k1-k2��0 | C�� | k2•k3��0 | D�� | k3��k2��k1 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com