练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    幂指函数y＝f(x)g(x)在求导数时，可以运用对数法：在函数解析式两边求对数得，两边求导数得＝，于是y′＝f(x)g(x)·．运用此法可以探求得知y＝的一个单调递增区间为(　　)．

    A．(0,2) B．(2,3) C．(e,4) D．(3, 8)

     

    A

    【解析】

    试题分析：由题可知对原函数两边取对数可得，两边对求导可得，即，对于时，,,,故，为单调递增区间．

    考点：导数的运算．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2015届山东省菏泽市高二下学期期末考试文科数学试卷（解析版） 题型：解答题

    （Ⅰ）求证：+＜2

    （Ⅱ）已知a＞0，b＞0且a+b＞2，求证：，中至少有一个小于2．

     

    查看答案和解析>>

    科目：高中数学 来源：2015届山东省高二下学期期中考试理科数学试卷（解析版） 题型：解答题

    如图，棱柱ABCD－A1B1C1D1的所有棱长都等于2，∠ABC＝60°，平面AA1C1C⊥平面ABCD，∠A1AC＝60°．

    (1)证明：BD⊥AA1；

    (2)求锐二面角D－A1A－C的平面角的余弦值；

    (3)在直线CC1上是否存在点P，使BP∥平面DA1C1？若存在，求出点P的位置；若不存在，说明理由．

     

    查看答案和解析>>

    科目：高中数学 来源：2015届山东省高二下学期期中考试理科数学试卷（解析版） 题型：选择题

    在下列命题中：

    ①若向量a，b共线，则向量a，b所在的直线平行；

    ②若向量a，b所在的直线为异面直线，则向量a，b一定不共面；

    ③若三个向量a，b，c两两共面，则向量a，b，c共面；

    ④已知空间的三个向量a，b，c，则对于空间的任意一个向量p总存在实数x，y，z使得p＝xa＋yb＋zc．

    其中正确命题的个数是(　　)

    A．0　　　　　 B．1 C．2 D．3

     

    查看答案和解析>>

    科目：高中数学 来源：2015届山东省高二下学期期中考试文科数学试卷（解析版） 题型：填空题

    已知定义在R上的偶函数满足：f(x＋4)＝f(x)＋f(2)，且当x∈[0,2]时，y＝f(x)单调递减，给出以下四个命题：

    ①f(2)＝0；

    ②x＝－4为函数y＝f(x)图象的一条对称轴；

    ③函数y＝f(x)在[8,10]上单调递增；

    ④若方程f(x)＝m在[－6，－2]上的两根为x1，x2则x1＋x2＝－8．以上命题中所有正确命题的序号为________．

     

    查看答案和解析>>

    科目：高中数学 来源：2015届山东省高二下学期期中考试文科数学试卷（解析版） 题型：选择题

    函数的值域是(　　)

    A．(－1,0)∪(0,1) B．[－1,1] C．(－1,1) D．[－1,0]∪(0,1)

     

    查看答案和解析>>

    科目：高中数学 来源：2015届山东省高二下学期期中考试理科数学试卷（解析版） 题型：解答题

    已知动圆()

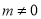    （1）当时，求经过原点且与圆相切的直线的方程；

    （2）若圆恰在圆的内部，求实数的取值范围.

     

    查看答案和解析>>

    科目：高中数学 来源：2015届山东省高二下学期期中考试理科数学试卷（解析版） 题型：选择题

    若直线与直线平行，则的值为（ ）

    A. B. C. D.

     

    查看答案和解析>>

    科目：高中数学 来源：2015届山东省高二下学期期中检测理科数学试卷（解析版） 题型：选择题

    由直线x＝－，x＝，y＝0与曲线y＝cosx所围成的封闭图形的面积为( )

    A． B．1 C． D．

     

    查看答案和解析>>

    同步练习册答案