Question

5．有一椭圆形溜冰场，长轴长100m，短轴长60m．现要在这溜冰场上划定一个各顶点都在溜冰场边界上的矩形区域，且使这个区域的面积最大，应把这个矩形的顶点定位在何处？这时矩形的周长是多少？

Answer 1

分析 分别以椭圆的长轴、短轴各自所在的直线为x轴和y轴，如图建立平面直角坐标系xOy，设矩形ABCD的各顶点都在椭圆上．利用矩形与椭圆的对称性可得：矩形ABCD关于原点O及x轴、y轴都对称．由已知可得：椭圆的方程为 $\frac{x^2}{{{{50}^2}}}+\frac{y^2}{{{{30}^2}}}=1$．设顶点A的坐标为（x₀，y₀），x₀＞0，y₀＞0，可得$y_0^2=\frac{{{{30}^2}}}{{{{50}^2}}}（{50^2}-x_0^2）$，根据矩形ABCD的对称性，可知它的面积S=4x₀y₀．代入利用二次函数的单调性可得：${x}_{0}^{2}{y}_{0}^{2}$的最大值，即可得出．

解答 解：分别以椭圆的长轴、短轴各自所在的直线为x轴和y轴，如图建立平面直角坐标系xOy，设矩形ABCD的各顶点都在椭圆上．
因为矩形的各顶点都在椭圆上，而矩形是中心对称图形，又是以过对称中心且垂直其一边的直线为对称轴的轴对称图形，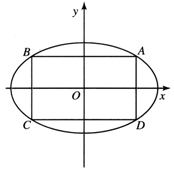
所以矩形ABCD关于原点O及x轴、y轴都对称．
已知椭圆的长轴长2a=100（m），短轴长2b=60（m），
则椭圆的方程为 $\frac{x^2}{{{{50}^2}}}+\frac{y^2}{{{{30}^2}}}=1$．
设顶点A的坐标为（x₀，y₀），x₀＞0，y₀＞0，
则$\frac{x_0^2}{{{{50}^2}}}+\frac{y_0^2}{{{{30}^2}}}=1$，得$y_0^2=\frac{{{{30}^2}}}{{{{50}^2}}}（{50^2}-x_0^2）$，
根据矩形ABCD的对称性，可知它的面积S=4x₀y₀．
由$x_0^2y_0^2=x_0^2•\frac{{{{30}^2}}}{{{{50}^2}}}（{50^2}-x_0^2）=\frac{{{{30}^2}}}{{{{50}^2}}}（-x_0^4+{50^2}x_0^2）=\frac{{{{30}^2}}}{{{{50}^2}}}[-{（x_0^2-\frac{{{{50}^2}}}{2}）^2}+\frac{{{{50}^4}}}{4}）$
因此，当$x_0^2=\frac{{{{50}^2}}}{2}$时，$x_0^2y_0^2$达到最大值，同时S=4x₀y₀也达到最大值．
这时${x_0}=25\sqrt{2}，{y_0}=15\sqrt{2}$．
矩形ABCD的周长为$4（{x_0}+{y_0}）=4（25\sqrt{2}+15\sqrt{2}）=160\sqrt{2}$（m）．
因此在溜冰场椭圆的短轴两侧分别画一条与短轴平行且与短轴相距$25\sqrt{2}$m（约35.35m）的直线，这两条直线与椭圆的交点就是所划定的矩形区域的顶点；这个矩形区域的周长为$160\sqrt{2}$m（约等于226.27m）．

点评 本题考查了椭圆的标准方程及其性质、矩形的对称性面积、二次函数的单调性，考查了推理能力与计算能力，属于难题．