
分析 (1)利用三角形的面积公式化简已知等式的左边,利用余弦定理表示出cosA,变形后代入等式的右边,利用同角三角函数间的基本关系弦化切整理后求出tanA的值,由A为三角形的内角,利用特殊角的三角函数值即可求出A的度数;
(2)由题意画出图形,可知三角形外接圆的半径为1,求解三角形可得BD,DC的值,进一步求得线段AD的长取值范围.
解答 解:(1)∵c2+b2-a2=4,S△ABC=4×$\frac{1}{2}$bc•sinA=2bc•sinA,
cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$,即b2+c2-a2=2bc•cosA
∴2bc•cosA=2bc•sinA
∴tanA=1
又0<A<π,
∴A=$\frac{π}{4}$.
(2)如图,△ABC的外接圆的半径为1,由题意可得BC=$\sqrt{2}$,OB⊥OC,
可知当D、O、A共线时,AD最大.
∵DC=$\sqrt{3}BD$,∴$(\sqrt{3}+1)BD=\sqrt{2}$,
∴$BD=\frac{\sqrt{2}}{\sqrt{3}+1}=\frac{\sqrt{6}-\sqrt{2}}{2}$,
$CD=\sqrt{2}-\frac{\sqrt{6}-\sqrt{2}}{2}=\frac{3\sqrt{2}-\sqrt{6}}{2}$,
在△COD中,∠OCD=45°,
OD=$\sqrt{{1}^{2}+(\frac{3\sqrt{2}-\sqrt{6}}{2})^{2}-2×\frac{3\sqrt{2}-\sqrt{6}}{2}×\frac{\sqrt{2}}{2}}=\sqrt{3}-1$.
∴BD<AD≤$\sqrt{3}-1+1=\sqrt{3}$.
即$\frac{\sqrt{6}-\sqrt{2}}{2}$<AD$≤\sqrt{3}$.
点评 本题考查了三角形的面积公式,余弦定理以及特殊角的三角函数值,熟练掌握公式及定理是解本题的关键,是中档题.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:填空题
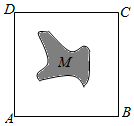 如图,面积为S的正方形ABCD中有一个不规则的图形M,可以用随机模拟方法近似计算M的面积,在正方向ABCD中随机投掷3600个点,若恰好有1200个点落入M中,则M的面积的近似值为$\frac{S}{3}$.
如图,面积为S的正方形ABCD中有一个不规则的图形M,可以用随机模拟方法近似计算M的面积,在正方向ABCD中随机投掷3600个点,若恰好有1200个点落入M中,则M的面积的近似值为$\frac{S}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{6}}{4}$ | B. | $\frac{5}{13}$ | C. | $\frac{\sqrt{3}}{4}$ | D. | $\frac{\sqrt{6}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知函数f(x)的部分图象如图所示,向图中的矩形区域随机投出200粒豆子,记下落入阴影区域的豆子数,通过100次这样的试验,算得落入阴影区域的豆子的平均数为66,由此可估计$\int_0^2{f(x)dx}$的值约为( )
已知函数f(x)的部分图象如图所示,向图中的矩形区域随机投出200粒豆子,记下落入阴影区域的豆子数,通过100次这样的试验,算得落入阴影区域的豆子的平均数为66,由此可估计$\int_0^2{f(x)dx}$的值约为( )| A. | $\frac{99}{25}$ | B. | $\frac{99}{50}$ | C. | $\frac{3}{10}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$+2 | B. | $\sqrt{3}$+3 | C. | 2$\sqrt{3}$+4 | D. | $\sqrt{3}$+4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com