
分析 由正数x,y满足$\frac{1}{x}+\frac{1}{y}=1$得到x-1=$\frac{1}{y-1}$,代入利用基本不等式可得.
解答 解:∵正数x,y满足$\frac{1}{x}+\frac{1}{y}=1$,
∴x=$\frac{y}{y-1}$,y>1,
∴x-1=$\frac{1}{y-1}$,
∴$\frac{1}{x-1}+\frac{4}{y-1}$=(y-1)+$\frac{4}{y-1}$≥2$\sqrt{(y-1)•\frac{4}{y-1}}$=4,当且仅当当y=3,x=$\frac{3}{2}$时取等号,
∴则$\frac{1}{x-1}+\frac{4}{y-1}$的最小值等于4,
故答案为:4.
点评 本题考查了基本不等式的应用,属于基础题


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
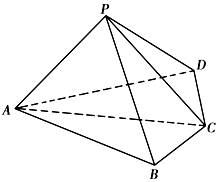 如图,四棱锥P-ABCD中,平面PAC⊥平面ABCD,AC=2BC=2CD=4,∠ACB=∠ACD=60°.
如图,四棱锥P-ABCD中,平面PAC⊥平面ABCD,AC=2BC=2CD=4,∠ACB=∠ACD=60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=2x+3 | B. | y=2x-3 | C. | y=-2x+3 | D. | y=-2x-3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
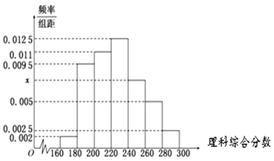 某重点中学100位学生在市统考中的理科综合分数,以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图.
某重点中学100位学生在市统考中的理科综合分数,以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com