
分析 (1)根据(2x-3)n展开式的二项式系数和求出n的值,化(2x-3)6=[-1+2(x-1)]6,求出a2的值;
(2)在(2x-3)6=[-1+2(x-1)]6=a0+a1(x-1)+a2(x-1)2+…+a9(x-1)6中,令x=0即可求出|a0|+|a1|+|a2|+|a3|+…|an|的值.
解答 解:(1)f(x)=(2x-3)n展开式的二项式系数和为64,
∴2n=64,解得n=6;
∵(2x-3)6=[-1+2(x-1)]6=a0+a1(x-1)+a2(x-1)2+…+a9(x-1)6,
∴a2=${C}_{6}^{2}$•(-1)4•22=60;
(2)在(2x-3)6=a0+a1(x-1)+a2(x-1)2+…+a6(x-1)6中,
即[-1+2(x-1)]6=a0+a1(x-1)+a2(x-1)2+…+a9(x-1)6,
令x=0,可得|a0|+|a1|+|a2|+|a3|+…|an|=(-1-2)6=729.
点评 本题考查了二项式定理以及二项展开式的通项公式应用问题,是基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
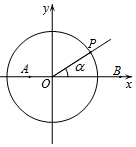 如图,在平面直角坐标系中,点$A(-\frac{1}{2},0)$,$B(\frac{3}{2},0)$,锐角α的终边与单位圆O交于点P.
如图,在平面直角坐标系中,点$A(-\frac{1}{2},0)$,$B(\frac{3}{2},0)$,锐角α的终边与单位圆O交于点P.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com