
分析 (1)由题意可得a,再由离心率公式和a,b,c的关系,解方程可得b,进而得到椭圆方程;
(2)联立直线与椭圆方程,直线 方程代入椭圆方程,求出交点坐标,利用距离公式求解即可.
解答 解:(1)由题意可得a=$\sqrt{{b}^{2}+{c}^{2}}$=$\sqrt{3}$,
e=$\frac{c}{a}$=$\frac{\sqrt{6}}{3}$,解得b=1,c=$\sqrt{2}$,
可得椭圆的方程为:$\frac{x^2}{3}+{y^2}=1$;
(2)直线l:y=x+1,
代入椭圆方程x2+3y2=3,
可得4x2+6x+3=3,
设A(x1,y1),B(x2,y2),
即有x1=0,x2=-$\frac{3}{2}$,y1=1,y2=-$\frac{1}{2}$,
可得弦长|AB|=$\sqrt{(0+\frac{3}{2})^{2}+(1+\frac{1}{2})^{2}}$=$\frac{{3\sqrt{2}}}{2}$.
点评 本题考查椭圆的方程的求法,注意运用离心率公式和a,b,c的关系,考查直线和椭圆方程联立,两点间距离公式的应用,考查运算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
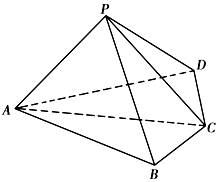 如图,四棱锥P-ABCD中,平面PAC⊥平面ABCD,AC=2BC=2CD=4,∠ACB=∠ACD=60°.
如图,四棱锥P-ABCD中,平面PAC⊥平面ABCD,AC=2BC=2CD=4,∠ACB=∠ACD=60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
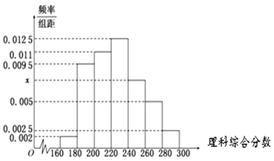 某重点中学100位学生在市统考中的理科综合分数,以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图.
某重点中学100位学生在市统考中的理科综合分数,以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0<x<2或x>4} | B. | {x|x<0或x>4} | C. | {x|0<x<2或x>2} | D. | {x|0<x<2或2<x<4} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{6}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com