设P是边长为a的正△ABC内的一点,P点到三边的距离分别为h1、h2、h3,则h1+h2+h3=
a;类比到空间,设P是棱长为a的空间正四面体ABCD内的一点,则P点到四个面的距离之和h1+h2+h3+h4= .
科目：高中数学 来源： 题型：填空题
已知函数f(x)在[0,1]上有意义，且f(0)＝f(1)，如果对任意的x1，x2∈[0,1]
且x1≠x2，都有|f(x1)－f(x2)|<|x1－x2|，求证：|f(x1)－f(x2)|<
，若用反证法证明该题，则反设应为________．
查看答案和解析>>
科目：高中数学 来源： 题型：填空题
在平面直角坐标系中,若点P(x,y)的坐标x,y均为整数,则称点P为格点.若一个多边形的顶点全是格点,则称该多边形为格点多边形.格点多边形的面积记为S,其内部的格点数记为N,边界上的格点数记为L.例如图中△ABC是格点三角形,对应的S=1,N=0,L=4.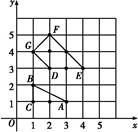
(1)图中格点四边形DEFG对应的S,N,L分别是 ;
(2)已知格点多边形的面积可表示为S=aN+bL+c,其中a,b,c为常数.若某格点多边形对应的N=71,L=18,则S= (用数值作答).
查看答案和解析>>
科目：高中数学 来源： 题型：填空题
在正整数数列中，由1开始依次按如下规则取它的项：第一次取1，第二次取2个连续偶数2、4；第三次取3个连续奇数5、7、9；第四次取4个连续偶数10、12、14、16；第五次取5个连续奇数17、19、21、23、25．按此规则一直取下去，得到一个子数列1，2，4，5，7，9，10,12，14，16，17，…．则在这个子数列中，由1开始的第15个数是 ，第2014个数是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
a
记该数组为：
,则
．
，则在下列的一段推理过程中，错误的推理步骤有 ．（填上所有错误步骤的序号）
<n，其中n>1且n∈N*，在验证n＝2时，式子的左边等于________．
＝2cos
，
＝2cos
，
＝2cos
，…，请从中归纳出第n个等式：＝________．