
【题目】已知曲线C的极坐标方程为ρ=![]() ,直线l的参数方程为
,直线l的参数方程为![]() (t为参数,0≤α<π).
(t为参数,0≤α<π).
(1)把曲线C的极坐标方程化为直角坐标方程,并说明曲线C的形状;
(2)若直线l经过点(1,0),求直线l被曲线C截得的线段AB的长.
【答案】(1)曲线C:y2=4x,顶点为O(0,0),焦点为F(1,0)的抛物线;(2)8
【解析】
(1)利用![]() 即可得出直角坐标方程;
即可得出直角坐标方程;
(2)直线l的参数方程![]() ( t为参数,0≤α<π).可得l经过点(0,1);若直线l经过点(1,0),得到
( t为参数,0≤α<π).可得l经过点(0,1);若直线l经过点(1,0),得到![]() ,得到直线l新的参数方程为
,得到直线l新的参数方程为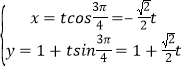 (t为参数).代入抛物线方程可得
(t为参数).代入抛物线方程可得![]() t+2=0,设A、B对应的参数分别为t1,t2,利用|AB|
t+2=0,设A、B对应的参数分别为t1,t2,利用|AB|![]() 即可得出.
即可得出.
(1)曲线C的极坐标方程ρ=![]() 化为ρ2sin2θ=4ρcosθ,
化为ρ2sin2θ=4ρcosθ,
得到曲线C的直角坐标方程为y2=4x,
故曲线C是顶点为O(0,0),焦点为F(1,0)的抛物线;
(2)直线l的参数方程为![]() ( t为参数,0≤α<π).
( t为参数,0≤α<π).
故l经过点(0,1);
若直线l经过点(1,0),则![]() ,
,
∴直线l的参数方程为 (t为参数).
(t为参数).
代入y2=4x,得![]() t+2=0
t+2=0
设A、B对应的参数分别为t1,t2,则t1+t2=﹣6![]() ,t1t2=2.
,t1t2=2.
|AB|=|t1﹣t2|=![]()
![]() =8.
=8.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知中心在原点的双曲线![]() 的右焦点为
的右焦点为![]() ,右顶点为
,右顶点为![]() .
.
(1)求双曲线![]() 的方程;
的方程;
(2)若直线![]() 与双曲线
与双曲线![]() 恒有两个不同的交点
恒有两个不同的交点![]() 和
和![]() ,且
,且![]() (其中
(其中![]() 为坐标原点),求实数
为坐标原点),求实数![]() 取值范围.
取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 的图象向右平移
的图象向右平移![]() 个单位,在向上平移一个单位,得到g(x)的图象.若g(x1)g(x2)=4,且x1,x2∈[﹣2π,2π],则x1﹣2x2的最大值为( )
个单位,在向上平移一个单位,得到g(x)的图象.若g(x1)g(x2)=4,且x1,x2∈[﹣2π,2π],则x1﹣2x2的最大值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,假命题的是( )
A.一条直线与两个平行平面中的一个相交,则必与另一个平面相交.
B.平行于同一平面的两条直线一定平行.
C.如果平面![]() 不垂直于平面
不垂直于平面![]() ,那么平面
,那么平面![]() 内一定不存在直线垂直于平面
内一定不存在直线垂直于平面![]() .
.
D.若直线![]() 不平行于平面
不平行于平面![]() ,且
,且![]() 不在平面
不在平面![]() 内,则在平面
内,则在平面![]() 内不存在与
内不存在与![]() 平行的直线.
平行的直线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() .
.
(1)若直线![]() 经过抛物线
经过抛物线![]() 的焦点,求抛物线
的焦点,求抛物线![]() 的准线方程;
的准线方程;
(2)若斜率为-1的直线经过抛物线![]() 的焦点
的焦点![]() ,且与抛物线
,且与抛物线![]() 交于
交于![]() ,
,![]() 两点,当
两点,当![]() 时,求抛物线
时,求抛物线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥![]() 中,底面是边长为4的正三角形,
中,底面是边长为4的正三角形,![]() 底面
底面![]() ,点
,点![]() 分别为
分别为![]() 的中点,且异面直线
的中点,且异面直线![]() 和
和![]() 所成的角的大小为
所成的角的大小为![]() .
.
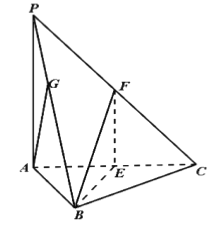
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com