
 已知抛物线C:y2=2px的准线为x=-$\frac{1}{2}$,过点(3,0)的直线l与抛物线C交于A,B两点,过线段AB的中点M作y轴的垂线交抛物线C于点N,直线AN,BN分别与抛物线的准线交于P,Q两点.
已知抛物线C:y2=2px的准线为x=-$\frac{1}{2}$,过点(3,0)的直线l与抛物线C交于A,B两点,过线段AB的中点M作y轴的垂线交抛物线C于点N,直线AN,BN分别与抛物线的准线交于P,Q两点.分析 (1)由抛物线C:y2=2px的准线为x=-$\frac{1}{2}$,∴p=1,即可得抛物线C的方程
(2)设A(x1,y1),B(x2,y2),则M($\frac{{x}_{1}+{x}_{2}}{2}$,$\frac{{y}_{1}+{y}_{2}}{2}$)由题意得$\left\{\begin{array}{l}{{y}^{2}=2x}\\{x=my+3}\end{array}\right.$,消去y得y2-2my-6=0
$\frac{{S}_{△NAB}}{{S}_{△NPQ}}$=$\frac{\frac{1}{2}NB•NA•sin∠ANB}{\frac{1}{2}NP•NQ•sin∠PNQ}=\frac{NB•NA}{NP•NQ}$=|$\frac{4{x}_{1}{x}_{2}-2{m}^{2}({x}_{1}+{x}_{2})+{m}^{4}}{{(m}^{2}+1)^{2}}$=|$\frac{({x}_{1}-\frac{{m}^{2}}{2})({x}_{2}-\frac{{m}^{2}}{2})}{(\frac{{m}^{2}}{2}+\frac{1}{2})(\frac{{m}^{2}}{2}+\frac{1}{2})}$|=|$\frac{3({m}^{2}+1)^{2}+6({m}^{2}+1)-45}{({m}^{2}+1)^{2}}$|令$\frac{1}{{m}^{2}+1}=t,t∈(0,1]$,则$\frac{{S}_{△NAB}}{{S}_{△NPQ}}$=|$\frac{3({m}^{2}+1)^{2}+6({m}^{2}+1)-45}{({m}^{2}+1)^{2}}$|=f(t)=|-45t2+6t+3|
即可求得△NAB和△NPQ的面积之比$\frac{{S}_{△NAB}}{{S}_{△NPQ}}$的最大值
解答 解:(1)∵抛物线C:y2=2px的准线为x=-$\frac{1}{2}$,∴p=1,抛物线C的方程为:y2=2x.
(2)设A(x1,y1),B(x2,y2),则M($\frac{{x}_{1}+{x}_{2}}{2}$,$\frac{{y}_{1}+{y}_{2}}{2}$)
由题意得$\left\{\begin{array}{l}{{y}^{2}=2x}\\{x=my+3}\end{array}\right.$,消去y得y2-2my-6=0
∴y1+y2=2m,y1y2=-6,则N($\frac{{m}^{2}}{2},m$)
$\frac{{S}_{△NAB}}{{S}_{△NPQ}}$=$\frac{\frac{1}{2}NB•NA•sin∠ANB}{\frac{1}{2}NP•NQ•sin∠PNQ}=\frac{NB•NA}{NP•NQ}$=|$\frac{4{x}_{1}{x}_{2}-2{m}^{2}({x}_{1}+{x}_{2})+{m}^{4}}{{(m}^{2}+1)^{2}}$=|$\frac{({x}_{1}-\frac{{m}^{2}}{2})({x}_{2}-\frac{{m}^{2}}{2})}{(\frac{{m}^{2}}{2}+\frac{1}{2})(\frac{{m}^{2}}{2}+\frac{1}{2})}$|=|$\frac{3({m}^{2}+1)^{2}+6({m}^{2}+1)-45}{({m}^{2}+1)^{2}}$|令$\frac{1}{{m}^{2}+1}=t,t∈(0,1]$,则$\frac{{S}_{△NAB}}{{S}_{△NPQ}}$=|$\frac{3({m}^{2}+1)^{2}+6({m}^{2}+1)-45}{({m}^{2}+1)^{2}}$|=f(t)=|-45t2+6t+3|
∵f(1)=36$>f(\frac{1}{15})$
∴当t=1时,△NAB和△NPQ的面积之比$\frac{{S}_{△NAB}}{{S}_{△NPQ}}$的最大值为36.
点评 本题考查了抛物线的方程,直线与抛物线的位置关系,考查了方程思想、计算能力,属于中档题


科目:高中数学 来源: 题型:选择题
| A. | y=f(x)的图象关于y轴对称 | B. | y=f(x)的极小值为-2 | ||
| C. | y=f(x)的极大值为-2 | D. | y=f(x)在(0,2)上是增函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
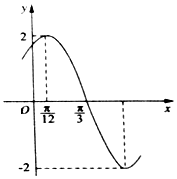 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,下列说法正确的是( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,下列说法正确的是( )| A. | 函数f(x)的图象关于直线x=-$\frac{2π}{3}$对称 | |
| B. | 函数f(x)的图象关于点(-$\frac{11π}{12}$,0)对称 | |
| C. | 若方程f(x)=m在[-$\frac{π}{2}$,0]上有两个不相等的实数根,则实数m∈(-2,-$\sqrt{3}$] | |
| D. | 将函数f(x)的图象向左平移$\frac{π}{6}$个单位可得到一个偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com