练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若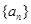是等差数列，首项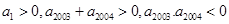，则使前n项和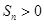成立的最大自然数n是：（   ）

    A．4005 B．4006 C．4007 D．4008

    B

    解析试题分析：根据题意可知：此等差数列的1到2003项每一项都大于0，从第2004项开始每一项都小于0，然后利用等差数列的前n项和公式表示出前4006项的和与前4007项的和，分别利用等差数列的性质变形后，根据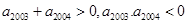，判断出前4005项的和为正与前4008项的和为负，即可求出满足题意的最大自然数n的值．
    由题意知：等差数列中，从第1项到第2003项是正数，且从第2004项开始为负数，结合通项公式和前n项和的关系可知，则前
    故可知n的最大值为4006，选B
    考点：等差数列的性质
    点评：此题考查了等差数列的性质及等差数列的通项公式．本小题结论可以推广成一般结论：等差数列中，a1＞0，ak+ak+1＞0，且akak+1＜0，则使前n项和Sn＞0的最大自然数n是2k．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：单选题

    已知数列，，，成等差数列, ，,,,成等比数列，则的值为(     )

    A． B． C．或 D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    一个样本容量为的样本数据，它们组成一个公差不为的等差数列，若且前项和，则此样本的平均数和中位数分别是 

    A． B． C． D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    等差数列:1,4,7,……中,当时,序号等于

    A．99 B．100 C．96 D．101

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    若是等差数列，首项公差，，且,则使数列的前n项和成立的最大自然数n是                           （   ）

    A．4027 B．4026 C．4025 D．4024

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    已知两个正数a，b的等差中项为4，则a，b的等比中项的最大值为(　　)

    A．2B．4C．8D．16

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    若数列是等差数列，且，则数列的前项和等于

    A． B．18 C．27 D．36

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    等差数列{an}的通项公式为an=2n+1，其前n项和为Sn，则{}前10项和为

    A．120B．100C．75D．70

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    在数列中，，，则等于（   ）

    A． B． C． D． 

    查看答案和解析>>

    同步练习册答案