练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知：如图，O1与O2外切于点P，经过O1上一点A作O1的切线交O2于B、C两点，直线AP交O2于点D，连接DC、PC．
    求证：DC2=DP•DA．精英家教网
    分析：相切两圆常作的辅助线是：两圆的公切线，因此过点P作两圆的内公切线EP交AB于点F，然后证得△CDP∽△ADC，可得证．
    解答：证明：过点P作两圆的内公切线EP交AB于点F，
    ∵FE、CA都与圆O1相切，精英家教网
    ∴EP=FA，
    ∴∠FAP=∠FPA；
    ∵∠FPA=∠EPA=∠DCP，
    ∴∠FAP=∠DCP；
    ∵∠PDC=∠CDA，
    ∴△CDP∽△ADC；
    ∴
    CD
    AD
    =
    DP
    CD
    ；
    ∴DC2=DP•DA．
    点评：将圆的有关知识与三角形相似结合考查，有一定难度；命题立意：此题主要考查相切两圆的位置关系及弦切角定理，三角形相似的判定等知识．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    选做题（请考生在以下三个小题中任选一题作答，如果多做，则按所做的第一题评阅记分）
    （1）（不等式选讲）已知函数f（x）=log2（|x-1|+|x-5|-a），当函数f（x）的定义域为R时，则实数a的取值范围为
    （-∞，4）
    （-∞，4）

    （2）（几何证明选讲）如图，AB是半圆O的直径，点C在半圆上，CD⊥AB，垂足为D，且AD=5DB，设∠COD=θ，则tanθ的值为
    		5
    2
    		5
    2
    ．

    （3）（坐标系与参数方程）圆O1和圆O2的极坐标方程分别为ρ=4cosθ，ρ=-4sinθ，则经过两圆圆心的直线的直角坐标方程为
    y=x+2
    y=x+2
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012•徐州模拟）本题包括A、B、C、D四小题，请选定其中两题，并在答题卡指定区域内作答，
    若多做，则按作答的前两题评分．解答时应写出文字说明、证明过程或演算步骤．
    A．选修4-1：几何证明选讲
    如图，半径分别为R，r（R＞r＞0）的两圆⊙O，⊙O1内切于点T，P是外圆⊙O上任意一点，连PT交⊙O1于点M，PN与内圆⊙O1相切，切点为N．求证：PN：PM为定值．
    B．选修4-2：矩阵与变换
    已知矩阵M=
    21
    34

    （1）求矩阵M的逆矩阵；
    （2）求矩阵M的特征值及特征向量；
    C．选修4-2：矩阵与变换
    在平面直角坐标系x0y中，求圆C的参数方程为
    x=-1+rcosθ
    y=rsinθ
    (θ    为参数r＞0），以O为极点，x轴正半轴为极轴建立极坐标系，直线l的极坐标方程为ρcos(θ+
    π
    4
    )=2
    		2
    ．若直线l与圆C相切，求r的值．
    D．选修4-5：不等式选讲
    已知实数a，b，c满足a＞b＞c，且a+b+c=1，a2+b2+c2=1，求证：1＜a+b＜
    4
    3
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知正三棱柱ABC-A1B1C1，底面边长AB=2，AB1⊥BC1，点O、O1分别是边AC，A1C1的中点，建立如图所示的空间直角坐标系．
    （1）求正三棱柱的侧棱长；
    （2）若M为BC1的中点，试用基向量
    AA1
    、
    AB
    、
    AC
    表示向量
    AM
    ；
    （3）求异面直线AM与BC所成角．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

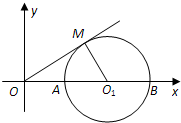    精英家教网如图，已知半径为1的⊙O1与x轴交于A，B两点，OM为⊙O1的切线，切点为M，且M在第一象限，圆心O1的坐标为（2，0），二次函数y=-x2+bx+c的图象经过A，B两点．
    （1）求二次函数的解析式；
    （2）求切线OM的函数解析式；
    （3）线段OM上是否存在一点P，使得以P，O，A为顶点的三角形与△OO1M相似．若存在，请求出所有符合条件的点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源：2013届重庆市高二上学期期中理科数学试卷 题型：解答题

    已知正三棱柱ABC—A1B1C1，底面边长AB=2，AB1⊥BC1，点O、O1分别是边AC，A1C1的中点，建立如图所示的空间直角坐标系.

    ⑴求正三棱柱的侧棱长.

    ⑵若M为BC1的中点，试用基向量、、表示向量；

    ⑶求异面直线AB1与BC所成角的余弦值．

     

     

     

    查看答案和解析>>

    同步练习册答案