练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】过点的动直线l与y轴交于点，过点T且垂直于l的直线与直线相交于点M.

    （1）求M的轨迹方程；

    （2）设M位于第一象限，以AM为直径的圆与y轴相交于点N，且，求的值.

    【答案】（1）（2）4

    【解析】

    （1）动直线l过点和，可根据垂直求出直线，从而求出交点M的坐标，从而寻找横纵坐标的关系，求出点M的轨迹方程. （2）由题意可知：点N即为圆与y轴的切点，根据，可求出直线AM的斜率，进而求出直线AM的方程，从而求出的值.

    解：（1）∵，，当时，M的坐标为

    当时，，∴，∴的方程为

    由得，

    验证当时，也满足

    ∴M的坐标满足方程，即M的轨迹方程为

    （2）作轴于，轴于，则

    又A为抛物线的焦点，∴，故圆与y轴相切于点N

    ∵，∵，∴，∴直线AM的方程为

    联立，消去y整理得，解得或（舍），即

    ∵A为抛物线的焦点，∴

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥P﹣ABCD中，PB⊥平面ABCD，AB⊥BC，AD∥BC，AD＝2BC＝2，AB＝BC＝PB，点E为棱PD的中点.

    （1）求证：CE∥平面PAB；

    （2）求证：AD⊥平面PAB；

    （3）求二面角E﹣AC﹣D的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列命题中，错误命题是

    A. “若，则”的逆命题为真

    B. 线性回归直线必过样本点的中心

    C. 在平面直角坐标系中到点和的距离的和为的点的轨迹为椭圆

    D. 在锐角中，有

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】第41届世界博览会于2010年5月1日至10月31日，在中国上海举行，气势磅礴的中国馆——“东方之冠”令人印象深刻，该馆以“东方之冠，鼎盛中华，天下粮仓，富庶百姓”为设计理念，代表中国文化的精神与气质．其形如冠盖，层叠出挑，制似斗拱．它有四根高33.3米的方柱，托起斗状的主体建筑，总高度为60.3米，上方的“斗冠”类似一个倒置的正四棱台，上底面边长是139.4米，下底面边长是69.9米，则“斗冠”的侧面与上底面的夹角约为（ ）．

    A.B.C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系xOy中，曲线E的参数方程为（为参数），以O为极点，x轴非负半轴为极轴建立极坐标系，直线，的极坐标方程分别为，，交曲线E于点A，B，交曲线E于点C，D.

    （1）求曲线E的普通方程及极坐标方程；

    （2）求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知O为坐标原点，，，直线AG，BG相交于点G，且它们的斜率之积为.记点G的轨迹为曲线C.

    （1）若射线与曲线C交于点D，且E为曲线C的最高点，证明：.

    （2）直线与曲线C交于M，N两点，直线AM，AN与y轴分别交于P，Q两点.试问在x轴上是否存在定点T，使得以PQ为直径的圆恒过点T？若存在，求出T的坐标；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】向50名学生调查对A、B两事件的态度，有如下结果：赞成A的人数是全体的五分之三，其余的不赞成，赞成B的比赞成A的多3人，其余的不赞成；另外，对A、B都不赞成的学生数比对A、B都赞成的学生数的三分之一多1人. 问对A、B都赞成的学生有____________人

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为迎接“五一国际劳动节”，某商场规定购买超过6000元商品的顾客可以参与抽奖活动现有甲品牌和乙品牌的扫地机器人作为奖品，从这两种品牌的扫地机器人中各随机抽取6台检测它们充满电后的工作时长相关数据见下表（工作时长单位：分）

    机器序号

    1

    2

    3

    4

    5

    6

    甲品牌工作时长/分

    220

    180

    210

    220

    200

    230

    乙品牌工作时长/分

    200

    190

    240

    230

    220

    210

    （1）根据所提供的数据，计算抽取的甲品牌的扫地机器人充满电后工作时长的平均数与方差；

    （2）从乙品牌被抽取的6台扫地机器人中随机抽出3台扫地机器人，记抽出的扫地机器人充满电后工作时长不低于220分钟的台数为，求的分布列与数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

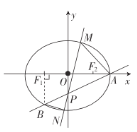
    【题目】如图，椭圆的右顶点为，左、右焦点分别为、，过点且斜率为的直线与轴交于点，与椭圆交于另一个点，且点在轴上的射影恰好为点．

    （1）求点的坐标；

    （2）过点且斜率大于的直线与椭圆交于两点，若，求实数的取值范围．

    查看答案和解析>>

    同步练习册答案