(1)证明:∵a
1=1,3tS
n-(2t+3)S
n-1=3t(n≥2,n∈N
*)①
∴3tS
n-1-(2t+3)S
n-2=3t(n≥3,n∈N*)②
①②两式相减得
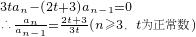
又n=2时,
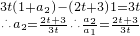
∴a
n是以1为首项,
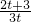
为公比的等比数列.
(2)解:∵
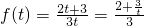
,∴
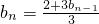
,∴
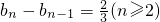
∴b
n是以1为首项,

为公差的等差数列,∴
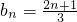
∴b
1b
2-b
2b
3+b
3b
4-b
4b
5+…+b
2n-1b
2n-b
2nb
2n+1(n∈N*)
=b
2(b
1-b
3)+b
4(b
3-b
4)+…+b
2n(b
2n-1-b
2n+1)
=
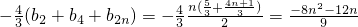
.
分析:(1)因为a
n=S
n-S
n-1(n≥2,n∈N
*),所以在3tS
n-(2t+3)S
n-1=3t的基础上,用n-1替换n构造与它类似的关系式;然后利用作差法求出a
n与a
n-1的关系式,进而可整理为等比数列形式;但不要忘掉未含项的检验.
(2)由(1)知{a
n}的公比f(t),又b
n=f(
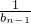
),则可找到b
n与b
n-1的关系,进而可整理为等差数列形式;则由等差数列通项公式可求b
n;代数式b
1b
2-b
2b
3+b
3b
4-b
4b
5+…+b
2n-1b
2n-b
2nb
2n+1的求值,可利用分组的方法,把它转化到等差数列的性质与前n项和公式上去,则问题解决.
点评:若数列{a
n}的前n项和为S
n,则a
n=S
n-S
n-1(n≥2,n∈N
*)是实现前n项和S
n向通项a
n转化的桥梁与纽带,进而可结合等差数列、等比数列的定义与性质解决问题.

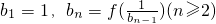 ,试求bn,并求b1b2-b2b3+b3b4-b4b5+…+b2n-1b2n-b2nb2n+1(n∈N*)
,试求bn,并求b1b2-b2b3+b3b4-b4b5+…+b2n-1b2n-b2nb2n+1(n∈N*)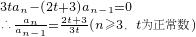
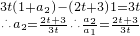
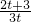 为公比的等比数列.
为公比的等比数列.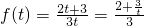 ,∴
,∴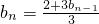 ,∴
,∴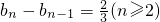
 为公差的等差数列,∴
为公差的等差数列,∴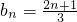
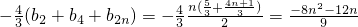 .
.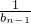 ),则可找到bn与bn-1的关系,进而可整理为等差数列形式;则由等差数列通项公式可求bn;代数式b1b2-b2b3+b3b4-b4b5+…+b2n-1b2n-b2nb2n+1的求值,可利用分组的方法,把它转化到等差数列的性质与前n项和公式上去,则问题解决.
),则可找到bn与bn-1的关系,进而可整理为等差数列形式;则由等差数列通项公式可求bn;代数式b1b2-b2b3+b3b4-b4b5+…+b2n-1b2n-b2nb2n+1的求值,可利用分组的方法,把它转化到等差数列的性质与前n项和公式上去,则问题解决.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案