
【题目】已知直线![]() 及点
及点![]() .
.
(1)求经过点![]() ,且与直线
,且与直线![]() 平行的直线方程;
平行的直线方程;
(2)求经过点![]() ,且倾斜角为直线
,且倾斜角为直线![]() 的倾斜角的
的倾斜角的![]() 倍的直线方程.
倍的直线方程.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆的中心在原点,焦点在![]() 轴上,离心率为
轴上,离心率为![]() ,若抛物线
,若抛物线![]() 的焦点与椭圆的一个焦点重合.
的焦点与椭圆的一个焦点重合.
(1)求椭圆的标准方程;
(2)过椭圆的左焦点![]() ,且斜率为
,且斜率为![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() ,
, ![]() 两点,求
两点,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn,点![]() (n∈N*)均在函数y=3x-2的图象上.
(n∈N*)均在函数y=3x-2的图象上.
(1)求数列{an}的通项公式;
(2)设bn=![]() ,Tn是数列{bn}的前n项和,求使得Tn<
,Tn是数列{bn}的前n项和,求使得Tn<![]() 对所有n∈N*都成立的最小正整数m.
对所有n∈N*都成立的最小正整数m.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阅读如下程序框图,如果输出i=5,那么在空白矩形框中应填入的语句为( ) 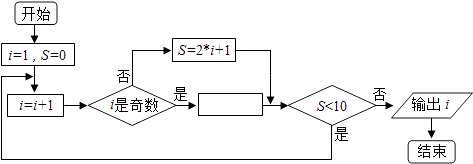
A.S=2*i﹣2
B.S=2*i﹣1
C.S=2*I
D.S=2*i+4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《张丘建算经》是我国南北朝时期的一部重要数学著作,书中系统的介绍了等差数列,同类结果在三百多年后的印度才首次出现.书中有这样一个问题,大意为:某女子善于织布,后一天比前一天织的快,而且每天增加的数量相同,已知第一天织布5尺,一个月(按30天计算)总共织布390尺,问每天增加的数量为多少尺?该问题的答案为( )
A.![]() 尺
尺
B.![]() 尺
尺
C.![]() 尺
尺
D.![]() 尺
尺
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(题文)平面内动点![]() 到两定点
到两定点![]() ,
,![]() 距离之比为常数
距离之比为常数![]() ,则动点
,则动点![]() 的轨迹叫做阿波罗尼斯圆.现已知定点
的轨迹叫做阿波罗尼斯圆.现已知定点![]() 、
、![]() ,圆心为
,圆心为![]() ,
,
(1)求满足上述定义的圆![]() 的方程,并指出圆心
的方程,并指出圆心![]() 的坐标和半径;
的坐标和半径;
(2)若![]() ,且经过点
,且经过点![]() 的直线
的直线![]() 交圆
交圆![]() 于
于![]() ,
,![]() 两点,当
两点,当![]() 的面积最大时,求直线
的面积最大时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】目前北方空气污染越来越严重,某大学组织学生参加环保知识竞赛,从参加学生中抽取40名,将其成绩(均为整数)整理后画出的频率分布直方图如图,若从成绩是80分以上(包括80分)的学生中选两人,则他们在同一分数段的概率为_______.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的焦点在
的焦点在![]() 轴上,离心率为
轴上,离心率为![]() ,抛物线
,抛物线![]() 的焦点在
的焦点在![]() 轴上,
轴上, ![]() 的中心和
的中心和![]() 的顶点均为原点,点
的顶点均为原点,点 在
在![]() 上,点
上,点![]() 在
在![]() 上,
上,
(1)求曲线![]() ,
, ![]() 的标准方程;
的标准方程;
(2)请问是否存在过抛物线![]() 的焦点
的焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同两点
交于不同两点![]() ,使得以线段
,使得以线段![]() 为直径的圆过原点
为直径的圆过原点![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com