
ΓΨΧβΡΩΓΩΡ≥Τσ“Β“ΜΧλ÷–≤ΜΆ§ ±ΩΧΒΡ”ΟΒγΝΩ![]() Θ®Άρ«ßΆΏ ±Θ©ΙΊ”Ύ ±Φδ
Θ®Άρ«ßΆΏ ±Θ©ΙΊ”Ύ ±Φδ![]() Θ®ΒΞΈΜΘΚ–Γ ±Θ§Τδ÷–
Θ®ΒΞΈΜΘΚ–Γ ±Θ§Τδ÷–![]() Ε‘”ΠΝη≥Ω0ΒψΘ©ΒΡΚ· ΐ
Ε‘”ΠΝη≥Ω0ΒψΘ©ΒΡΚ· ΐ![]() ΫϋΥΤ¬ζΉψ
ΫϋΥΤ¬ζΉψ![]()
![]() ,»γΆΦ «Κ· ΐ
,»γΆΦ «Κ· ΐ![]() ΒΡ≤ΩΖ÷ΆΦœσΘ°
ΒΡ≤ΩΖ÷ΆΦœσΘ°

Θ®1Θ©«σ![]() ΒΡΫβΈω ΫΘΜ
ΒΡΫβΈω ΫΘΜ
Θ®2Θ©“―÷ΣΗΟΤσ“ΒΡ≥Χλ«ΑΑκ»’ΡήΖ÷≈δΒΫΒΡΙ©ΒγΝΩ![]() Θ®Άρ«ßΆΏ ±Θ©”κ ±Φδ
Θ®Άρ«ßΆΏ ±Θ©”κ ±Φδ![]() Θ®–Γ ±Θ©ΒΡΙΊœΒΩ…”ΟœΏ–‘Κ· ΐΡΘ–Ά
Θ®–Γ ±Θ©ΒΡΙΊœΒΩ…”ΟœΏ–‘Κ· ΐΡΘ–Ά![]() ΡΘΡβΘ§Β±Ι©ΒγΝΩ
ΡΘΡβΘ§Β±Ι©ΒγΝΩ![]() –Γ”ΎΤσ“Β”ΟΒγΝΩ
–Γ”ΎΤσ“Β”ΟΒγΝΩ![]() ±Θ§Τσ“Β±Ί–κΆΘ≤ζΘ°≥θ≤Ϋ‘ΛΦΤΩΣ ΦΆΘ≤ζΒΡΝΌΫγ ±Φδ
±Θ§Τσ“Β±Ί–κΆΘ≤ζΘ°≥θ≤Ϋ‘ΛΦΤΩΣ ΦΆΘ≤ζΒΡΝΌΫγ ±Φδ![]() ‘Ύ÷–Έγ11ΒψΒΫ12Βψ÷°ΦδΘ§”ΟΕΰΖ÷Ζ®ΙάΥψ
‘Ύ÷–Έγ11ΒψΒΫ12Βψ÷°ΦδΘ§”ΟΕΰΖ÷Ζ®ΙάΥψ![]() Υυ‘ΎΒΡ“ΜΗω«χΦδΘ®«χΦδ≥ΛΕ»ΨΪ»ΖΒΫ15Ζ÷÷”Θ©Θ°
Υυ‘ΎΒΡ“ΜΗω«χΦδΘ®«χΦδ≥ΛΕ»ΨΪ»ΖΒΫ15Ζ÷÷”Θ©Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() ΘΜΘ®2Θ©
ΘΜΘ®2Θ©![]() .
.
ΓΨΫβΈωΓΩ
Θ®1Θ©”…ΆΦœσΘ§άϊ”ΟΉν¥σ÷Β”κΉν–Γ÷Β≤νΒΡ“ΜΑκ«σΒΟ![]() Θ§”…Ήν¥σ÷Β”κΉν–Γ÷ΒΚΆΒΡ“ΜΑκ«σΒΟ
Θ§”…Ήν¥σ÷Β”κΉν–Γ÷ΒΚΆΒΡ“ΜΑκ«σΒΟ![]() Θ§”…÷ήΤΎ«σΒΟ
Θ§”…÷ήΤΎ«σΒΟ![]() Θ§”…ΧΊ βΒψ«σΒΟ
Θ§”…ΧΊ βΒψ«σΒΟ![]() ΒΡ÷ΒΘ§¥”ΕχΩ…ΒΟ
ΒΡ÷ΒΘ§¥”ΕχΩ…ΒΟ![]() ΒΡΫβΈω ΫΘΜ Θ®2Θ©ΙΙ‘λΚ· ΐ
ΒΡΫβΈω ΫΘΜ Θ®2Θ©ΙΙ‘λΚ· ΐ![]() Θ§œ»≈–Εœ
Θ§œ»≈–Εœ![]() ‘Ύ
‘Ύ![]() …œ «ΒΞΒςΒί‘ωΚ· ΐΘ§‘Όάϊ”ΟΕΰΖ÷Ζ®≈–ΕœΚ· ΐ
…œ «ΒΞΒςΒί‘ωΚ· ΐΘ§‘Όάϊ”ΟΕΰΖ÷Ζ®≈–ΕœΚ· ΐ![]() ΒΡΝψΒψΥυ‘ΎΒΡ«χΦδΘ°
ΒΡΝψΒψΥυ‘ΎΒΡ«χΦδΘ°
Θ®1Θ©”…ΆΦœσΩ…÷ΣA=![]() =
=![]() Θ§B=
Θ§B=![]() =2Θ§T=12=
=2Θ§T=12=![]() Θ§ΠΊ=
Θ§ΠΊ=![]() Θ§
Θ§
¥ζ»κΒψΘ®0Θ§2.5Θ©ΒΟsinΠ’=1Θ§
ΓΏ0ΘΦΠ’ΘΦΠ–Θ§ΓύΠ’=![]() ΘΜ
ΘΜ
Ήέ…œΘ§A=![]() Θ§B=2Θ§ΠΊ=
Θ§B=2Θ§ΠΊ=![]() Θ§Π’=
Θ§Π’=![]() Θ§
Θ§
Φ¥fΘ®tΘ©=![]() sinΘ®
sinΘ®![]() t+
t+![]() Θ©+2.
Θ©+2.
Θ®2Θ©”…Θ®1Θ©÷ΣfΘ®tΘ©=![]() sinΘ®
sinΘ®![]() t+
t+![]() Θ©+2=
Θ©+2=![]() cos
cos![]() t+2Θ§
t+2Θ§
ΝνhΘ®tΘ©=fΘ®tΘ©-gΘ®tΘ©Θ§
…ηhΘ®t0Θ©=0Θ§‘ρt0ΈΣΗΟΤσ“ΒΒΡΩΣ ΦΆΘ≤ζΒΡΝΌΫγ ±ΦδΘΜ
“Ή÷ΣhΘ®tΘ©‘ΎΘ®11Θ§12Θ©…œ «ΒΞΒςΒί‘ωΚ· ΐΘΜ
”…hΘ®11Θ©=fΘ®11Θ©-gΘ®11Θ©=![]() cos
cos![]() +2+2ΓΝ11-25=
+2+2ΓΝ11-25=![]() -1ΘΦ0Θ§
-1ΘΦ0Θ§
hΘ®12Θ©=fΘ®12Θ©-gΘ®12Θ©=![]() cos
cos![]() +2+2ΓΝ12-25=
+2+2ΓΝ12-25=![]() ΘΨ0Θ§
ΘΨ0Θ§
”÷hΘ®11.5Θ©=fΘ®11.5Θ©-gΘ®11.5Θ©=![]() cos
cos![]() +2+2ΓΝ11.5-25=
+2+2ΓΝ11.5-25=![]() cosΘ®-
cosΘ®-![]() Θ©=
Θ©=![]() cos
cos![]() =
=![]() ΘΨ0Θ§
ΘΨ0Θ§
‘ρt0Γ Θ®11Θ§11.5Θ©Θ§Φ¥11ΒψΒΫ11Βψ30Ζ÷÷°ΦδΘ®¥σ”Ύ15Ζ÷÷”Θ©Θ§
”÷hΘ®11.25Θ©=fΘ®11.25Θ©-gΘ®11.25Θ©=![]() cos
cos![]() +2+2ΓΝ11.25-25ΘΦ
+2+2ΓΝ11.25-25ΘΦ![]() ΓΝ1-0.5=0Θ§
ΓΝ1-0.5=0Θ§
‘ρt0Γ Θ®11.25Θ§11.5Θ©Θ§Φ¥11Βψ15Ζ÷ΒΫ11Βψ30Ζ÷÷°ΦδΘ®’ΐΚΟ15Ζ÷÷”Θ©Θ°
Υυ“‘Θ§Τσ“ΒΩΣ ΦΆΘ≤ζΒΡΝΌΫγ ±Φδt0Υυ‘ΎΒΡ«χΦδΈΣΘ®11.25Θ§11.5Θ©.



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ…ηΓςABCΒΡΡΎΫ«AΘ§BΘ§CΥυΕ‘±ΏΖ÷±πΈΣaΘ§bΘ§cΘ§«“a+c=6Θ§b=2Θ§ ![]() Θ°
Θ°
Θ®1Θ©«σaΘ§cΒΡ÷ΒΘΜ
Θ®2Θ©«σsinΘ®A©¹BΘ©ΒΡ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ…ηœρΝΩ ![]() Θ§
Θ§ ![]() Θ§
Θ§ ![]() Θ°
Θ°
Θ®1Θ©»τ ![]() Θ§«σxΒΡ÷ΒΘΜ
Θ§«σxΒΡ÷ΒΘΜ
Θ®2Θ©…ηΚ· ΐ ![]() Θ§«σfΘ®xΘ©ΒΡΉν¥σ÷ΒΘ°
Θ§«σfΘ®xΘ©ΒΡΉν¥σ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ”…÷–―κΒγ ”Χ®ΉέΚœΤΒΒάΘ®![]() Θ©ΚΆΈ®÷Ύ¥ΪΟΫΝΣΚœ÷ΤΉςΒΡΓΕΩΣΫ≤ά≤ΓΖ «÷–Ιζ ΉΒΒ«ύ¥ΚΒγ ”ΙΪΩΣΩΈΓΘΟΩΤΎΫΎΡΩ”…“ΜΈΜ÷ΣΟϊ»Υ ΩΫ≤ ωΉ‘ΦΚΒΡΙ ¬Θ§Ζ÷œμΥϊΟ«Ε‘”Ύ…ζΜνΚΆ…ζΟϋΒΡΗ–ΈρΘ§Ηχ”η÷–Ιζ«ύΡξœ÷ ΒΒΡΧ÷¬έΚΆ–ΡΝιΒΡΉΧ―χΘ§Χ÷¬έ«ύΡξΟ«ΒΡ»Υ…ζΈ ΧβΘ§Ά§ ±“≤‘ΎΧ÷¬έ«ύ¥Κ÷–ΙζΒΡ…γΜαΈ ΧβΘ§ ήΒΫ«ύΡξΙέ÷ΎΒΡœ≤Α°Θ§ΈΣΝΥΝΥΫβΙέ÷ΎΕ‘ΫΎΡΩΒΡœ≤Α°≥ΧΕ»Θ§Βγ ”Χ®ΥφΜζΒς≤ιΝΥ
Θ©ΚΆΈ®÷Ύ¥ΪΟΫΝΣΚœ÷ΤΉςΒΡΓΕΩΣΫ≤ά≤ΓΖ «÷–Ιζ ΉΒΒ«ύ¥ΚΒγ ”ΙΪΩΣΩΈΓΘΟΩΤΎΫΎΡΩ”…“ΜΈΜ÷ΣΟϊ»Υ ΩΫ≤ ωΉ‘ΦΚΒΡΙ ¬Θ§Ζ÷œμΥϊΟ«Ε‘”Ύ…ζΜνΚΆ…ζΟϋΒΡΗ–ΈρΘ§Ηχ”η÷–Ιζ«ύΡξœ÷ ΒΒΡΧ÷¬έΚΆ–ΡΝιΒΡΉΧ―χΘ§Χ÷¬έ«ύΡξΟ«ΒΡ»Υ…ζΈ ΧβΘ§Ά§ ±“≤‘ΎΧ÷¬έ«ύ¥Κ÷–ΙζΒΡ…γΜαΈ ΧβΘ§ ήΒΫ«ύΡξΙέ÷ΎΒΡœ≤Α°Θ§ΈΣΝΥΝΥΫβΙέ÷ΎΕ‘ΫΎΡΩΒΡœ≤Α°≥ΧΕ»Θ§Βγ ”Χ®ΥφΜζΒς≤ιΝΥ![]() ΓΔ
ΓΔ![]() ΝΫΗωΒΊ«χΒΡ100ΟϊΙέ÷ΎΘ§ΒΟΒΫ»γœ¬ΒΡ
ΝΫΗωΒΊ«χΒΡ100ΟϊΙέ÷ΎΘ§ΒΟΒΫ»γœ¬ΒΡ![]() Ν–ΝΣ±μΘΚ
Ν–ΝΣ±μΘΚ
Ζ«≥Θ¬ζ“β | ¬ζ“β | ΚœΦΤ | |
| 30 |
| |
|
|
| |
ΚœΦΤ |
“―÷Σ‘Ύ±ΜΒς≤ιΒΡ100ΟϊΙέ÷Ύ÷–ΥφΜζ≥ι»Γ1ΟϊΘ§ΗΟΙέ÷Ύ «![]() ΒΊ«χΒ±÷–ΓΑΖ«≥Θ¬ζ“βΓ±ΒΡΙέ÷ΎΒΡΗ≈¬ ΈΣ
ΒΊ«χΒ±÷–ΓΑΖ«≥Θ¬ζ“βΓ±ΒΡΙέ÷ΎΒΡΗ≈¬ ΈΣ![]() Θ§«“
Θ§«“![]() .
.
Θ®ΔώΘ©œ÷¥”100ΟϊΙέ÷Ύ÷–”ΟΖ÷≤ψ≥ι―υΒΡΖΫΖ®≥ι»Γ20ΟϊΫχ––Έ ΨμΒς≤ιΘ§‘ρ”Π≥ι»ΓΓΑ¬ζ“βΓ±ΒΡ![]() ΓΔ
ΓΔ![]() ΒΊ«χΒΡ»Υ ΐΗς «Εύ…ΌΘΜ
ΒΊ«χΒΡ»Υ ΐΗς «Εύ…ΌΘΜ
Θ®ΔρΘ©Άξ≥……œ ω±μΗώΘ§≤ΔΗυΨί±μΗώ≈–Εœ «Ζώ”–![]() ΒΡΑ―Έ’»œΈΣΙέ÷ΎΒΡ¬ζ“β≥ΧΕ»”κΥυ‘ΎΒΊ«χ”–ΙΊœΒΘΜ
ΒΡΑ―Έ’»œΈΣΙέ÷ΎΒΡ¬ζ“β≥ΧΕ»”κΥυ‘ΎΒΊ«χ”–ΙΊœΒΘΜ
Θ®ΔσΘ©»τ“‘≥ι―υΒς≤ιΒΡΤΒ¬ ΈΣΗ≈¬ Θ§¥”![]() ΒΊ«χΥφΜζ≥ι»Γ3»ΥΘ§…η≥ιΒΫΒΡΙέ÷ΎΓΑΖ«≥Θ¬ζ“βΓ±ΒΡ»Υ ΐΈΣ
ΒΊ«χΥφΜζ≥ι»Γ3»ΥΘ§…η≥ιΒΫΒΡΙέ÷ΎΓΑΖ«≥Θ¬ζ“βΓ±ΒΡ»Υ ΐΈΣ![]() Θ§«σ
Θ§«σ![]() ΒΡΖ÷≤ΦΝ–ΚΆΤΎΆϊ.
ΒΡΖ÷≤ΦΝ–ΚΆΤΎΆϊ.
|
|
|
|
|
|
|
|
|
|
ΗΫΘΚ≤ΈΩΦΙΪ ΫΘΚ![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈΣΝΥΗϋΚΟΒΊΙφΜ°ΫχΜθΒΡ ΐΝΩΘ§±Θ÷Λ Ώ≤ΥΒΡ–¬œ ≥ΧΕ»Θ§Ρ≥ Ώ≤Υ…ΧΒξ¥”Ρ≥“ΜΡξΒΡœζ έ ΐΨί÷–Θ§ΥφΜζ≥ι»ΓΝΥ8Ήι ΐΨίΉςΈΣ―–ΨΩΕ‘œσΘ§»γ±μΥυ ΨΘ®![]() Θ®Ε÷Θ©ΈΣ¬ρΫχ Ώ≤ΥΒΡ ΐΝΩΘ§
Θ®Ε÷Θ©ΈΣ¬ρΫχ Ώ≤ΥΒΡ ΐΝΩΘ§![]() Θ®ΧλΘ©ΈΣœζ έΧλ ΐΘ©ΘΚ
Θ®ΧλΘ©ΈΣœζ έΧλ ΐΘ©ΘΚ
| 2 | 3 | 4 | 5 | 6 | 7 | 9 | 12 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
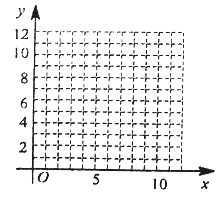
Θ®1Θ©ΗυΨί…œ±μ ΐΨί‘ΎΥυΗχΉχ±ξœΒ÷–Μφ÷Τ…ΔΒψΆΦΘ§≤Δ”ΟΉν–ΓΕΰ≥ΥΖ®«σ≥ω![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ΒΡœΏ–‘ΜΊΙιΖΫ≥Χ
ΒΡœΏ–‘ΜΊΙιΖΫ≥Χ![]() ΘΜ
ΘΜ
Θ®2Θ©ΗυΨίΘ®ΔώΘ©÷–ΒΡΦΤΥψΫαΙϊΘ§ΗΟ Ώ≤Υ…ΧΒξΉΦ±Η“Μ¥Έ–‘¬ρΫχ25Ε÷Θ§‘ΛΦΤ–η“Σœζ έΕύ…ΌΧλΘΩ
Θ®≤ΈΩΦ ΐΨίΚΆΙΪ ΫΘΚ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§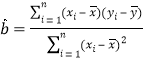
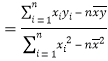 Θ§
Θ§![]() .Θ©
.Θ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ’ΐœν ΐΝ–{an}ΒΡ«ΑnœνΚΆSn¬ζΉψΘΚSn2 ![]()
Θ®1Θ©«σ ΐΝ–{an}ΒΡΆ®œνΙΪ ΫanΘΜ
Θ®2Θ©Ννb ![]() Θ§ ΐΝ–{bn}ΒΡ«ΑnœνΚΆΈΣTn Θ° ÷ΛΟςΘΚΕ‘”Ύ»Έ“βnΓ N* Θ§ ΕΦ”–
Θ§ ΐΝ–{bn}ΒΡ«ΑnœνΚΆΈΣTn Θ° ÷ΛΟςΘΚΕ‘”Ύ»Έ“βnΓ N* Θ§ ΕΦ”– ![]() Θ°
Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΦΉΓΔ““ΓΔ±ϊΓΔΕΓΥΡΈΜΆ§―ßΗΏΩΦ÷°ΚσΦΤΜ°»Ξ![]() »ΐΗω≤ΜΆ§…γ«χΫχ––ΑοΖωΜνΕ·Θ§ΟΩ»Υ÷ΜΡή»Ξ“ΜΗω…γ«χΘ§ΟΩΗω…γ«χ÷Ν…Ό“Μ»Υ.Τδ÷–ΦΉ±Ί–κ»Ξ
»ΐΗω≤ΜΆ§…γ«χΫχ––ΑοΖωΜνΕ·Θ§ΟΩ»Υ÷ΜΡή»Ξ“ΜΗω…γ«χΘ§ΟΩΗω…γ«χ÷Ν…Ό“Μ»Υ.Τδ÷–ΦΉ±Ί–κ»Ξ![]() …γ«χΘ§““≤Μ»Ξ
…γ«χΘ§““≤Μ»Ξ![]() …γ«χΘ§‘ρ≤ΜΆ§ΒΡΑ≤≈≈ΖΫΖ®÷÷ ΐΈΣ Θ® Θ©
…γ«χΘ§‘ρ≤ΜΆ§ΒΡΑ≤≈≈ΖΫΖ®÷÷ ΐΈΣ Θ® Θ©
A. 24 B. 8 C. 7 D. 6
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ ΐΝ–![]() ΒΡ«Α
ΒΡ«Α![]() œνΚΆΈΣ
œνΚΆΈΣ![]() Θ§«“
Θ§«“![]() .
.
Θ®1Θ©÷ΛΟς![]() «Β»±» ΐΝ–Θ§≤Δ«σ
«Β»±» ΐΝ–Θ§≤Δ«σ![]() ΒΡΆ®œνΙΪ ΫΘΜ
ΒΡΆ®œνΙΪ ΫΘΜ
Θ®2Θ©«σ![]() ΘΜ
ΘΜ
Θ®3Θ©…η![]() ,»τ
,»τ![]() Ε‘
Ε‘![]() Κψ≥…ΝΔΘ§«σ Β ΐ
Κψ≥…ΝΔΘ§«σ Β ΐ![]() ΒΡ»Γ÷ΒΖΕΈß.
ΒΡ»Γ÷ΒΖΕΈß.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΘ®±Ψ–ΓΧβ¬ζΖ÷12Ζ÷Θ©…ηΚ· ΐ![]() .
.
(Δώ)Χ÷¬έΚ· ΐ![]() ΒΡΒΞΒς–‘ΘΜ
ΒΡΒΞΒς–‘ΘΜ
(Δρ)Β±Κ· ΐ![]() ”–Ήν¥σ÷Β«“Ήν¥σ÷Β¥σ”Ύ
”–Ήν¥σ÷Β«“Ήν¥σ÷Β¥σ”Ύ![]() ±Θ§«σ
±Θ§«σ![]() ΒΡ»Γ÷ΒΖΕΈß.
ΒΡ»Γ÷ΒΖΕΈß.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com