
【题目】为了更好地规划进货的数量,保证蔬菜的新鲜程度,某蔬菜商店从某一年的销售数据中,随机抽取了8组数据作为研究对象,如表所示(![]() (吨)为买进蔬菜的数量,
(吨)为买进蔬菜的数量,![]() (天)为销售天数):
(天)为销售天数):
| 2 | 3 | 4 | 5 | 6 | 7 | 9 | 12 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
(1)根据上表数据在所给坐标系中绘制散点图,并用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据(Ⅰ)中的计算结果,该蔬菜商店准备一次性买进25吨,预计需要销售多少天?
(参考数据和公式:![]() ,
,![]() ,
,![]() ,
,![]() ,
,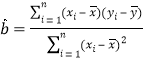
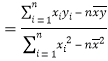 ,
,![]() .)
.)
科目:高中数学 来源: 题型:
【题目】某高校为调查学生喜欢“应用统计”课程是否与性别有关,随机抽取了选修课程的60名学生,得到数据如下表:
喜欢统计课程 | 不喜欢统计课程 | 合计 | |
男生 | 20 | 10 | 30 |
女生 | 10 | 20 | 30 |
合计 | 30 | 30 | 60 |
(1)判断是否有99.5%的把握认为喜欢“应用统计”课程与性别有关?
(2)用分层抽样的方法从喜欢统计课程的学生中抽取6名学生作进一步调查,将这6名学生作为一个样本,从中任选3人,求恰有2个男生和1个女生的概率.
下面的临界值表供参考:
| 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的左焦点为F,C与过原点的直线相交于A,B两点,连接AF、BF,若|AB|=10,|AF|=6,cos∠ABF=
的左焦点为F,C与过原点的直线相交于A,B两点,连接AF、BF,若|AB|=10,|AF|=6,cos∠ABF= ![]() ,则C的离心率e= .
,则C的离心率e= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面斜坐标系![]() 中,
中,![]() ,平面上任意一点
,平面上任意一点![]() 关于斜坐标系的斜坐标是这样定义的:若
关于斜坐标系的斜坐标是这样定义的:若![]() (其中
(其中![]() ,
,![]() 分别为与
分别为与![]() 轴,
轴,![]() 轴同方向的单位向量),则
轴同方向的单位向量),则![]() 点的斜坐标为
点的斜坐标为![]()

(1)若点![]() 在斜坐标系
在斜坐标系![]() 中的坐标为
中的坐标为![]() ,求点
,求点![]() 到原点
到原点![]() 的距离.
的距离.
(2)求以原点![]() 为圆心且半径为
为圆心且半径为![]() 的圆在斜坐标系
的圆在斜坐标系![]() 中的方程.
中的方程.
(3)在斜坐标系![]() 中,若直线
中,若直线![]() 交(2)中的圆于
交(2)中的圆于![]() 两点,则当
两点,则当![]() 为何值时,
为何值时,![]() 的面积取得最大值?并求此最大值.
的面积取得最大值?并求此最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业一天中不同时刻的用电量![]() (万千瓦时)关于时间
(万千瓦时)关于时间![]() (单位:小时,其中
(单位:小时,其中![]() 对应凌晨0点)的函数
对应凌晨0点)的函数![]() 近似满足
近似满足![]()
![]() ,如图是函数
,如图是函数![]() 的部分图象.
的部分图象.

(1)求![]() 的解析式;
的解析式;
(2)已知该企业某天前半日能分配到的供电量![]() (万千瓦时)与时间
(万千瓦时)与时间![]() (小时)的关系可用线性函数模型
(小时)的关系可用线性函数模型![]() 模拟,当供电量
模拟,当供电量![]() 小于企业用电量
小于企业用电量![]() 时,企业必须停产.初步预计开始停产的临界时间
时,企业必须停产.初步预计开始停产的临界时间![]() 在中午11点到12点之间,用二分法估算
在中午11点到12点之间,用二分法估算![]() 所在的一个区间(区间长度精确到15分钟).
所在的一个区间(区间长度精确到15分钟).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年5月14日.第一届“一带一路国际高峰论坛在北京举行,为了解不同年龄的人对“一带一路”关注程度,某机构随机抽取了年龄在15-75岁之间的100人进行调查,经统计“青少年”与“中老年” 的人数之比为9:11

(1)根据已知条件完成上面的列联表,并判断能否有99%的把握认为关注“一带一路”是和年龄段有关?
(2)现从抽取的青少年中采用分层抽样的办法选取9人进行问卷调查,在这9人中再取3人进打面对面询问,记选取的3人中“一带一路”的人数为X,求x的分布列及数学期望.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某社区为了解居民喜欢中华传统文化是否与年龄有关,随机调查了60位居民,相关数据统计如下表所示,
喜欢 | 不喜欢 | 合计 | |
大于45岁 | 26 | 6 | 32 |
25岁至45岁 | 13 | 15 | 28 |
合计 | 39 | 21 | 60 |
(Ⅰ)是否有99.5%以上的人把握认为喜欢中华传统文化与年龄有关?
(Ⅱ)按年龄采用分层抽样的方法从喜欢中华传统文化的受调查居民中随机抽取6人作进一步了解,若从这6位居民中任选2人,求这2人的年龄均大于45岁的概率.
附:![]()
![]()
| 0.025 | 0.010 | 0.005 | 0,001 |
| 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com