
【题目】已知![]() 为抛物线
为抛物线![]() 的焦点,
的焦点,![]() 为其标准线与
为其标准线与![]() 轴的交点,过
轴的交点,过![]() 的直线交抛物线
的直线交抛物线![]() 于
于![]() ,
,![]() 两点,
两点,![]() 为线段
为线段![]() 的中点,且
的中点,且![]() ,则
,则![]() __________.
__________.
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,点
,点![]() ,
,![]() 分别为椭圆
分别为椭圆![]() 的左右顶点,点
的左右顶点,点![]() 在
在![]() 上,且
上,且![]() 面积的最大值为
面积的最大值为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设![]() 为
为![]() 的左焦点,点
的左焦点,点![]() 在直线
在直线![]() 上,过
上,过![]() 作
作![]() 的垂线交椭圆
的垂线交椭圆![]() 于
于![]() ,
,![]() 两点.证明:直线
两点.证明:直线![]() 平分线段
平分线段![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由中央电视台综合频道(![]() )和唯众传媒联合制作的《开讲啦》是中国首档青春电视公开课。每期节目由一位知名人士讲述自己的故事,分享他们对于生活和生命的感悟,给予中国青年现实的讨论和心灵的滋养,讨论青年们的人生问题,同时也在讨论青春中国的社会问题,受到青年观众的喜爱,为了了解观众对节目的喜爱程度,电视台随机调查了
)和唯众传媒联合制作的《开讲啦》是中国首档青春电视公开课。每期节目由一位知名人士讲述自己的故事,分享他们对于生活和生命的感悟,给予中国青年现实的讨论和心灵的滋养,讨论青年们的人生问题,同时也在讨论青春中国的社会问题,受到青年观众的喜爱,为了了解观众对节目的喜爱程度,电视台随机调查了![]() 、
、![]() 两个地区的100名观众,得到如下的
两个地区的100名观众,得到如下的![]() 列联表:
列联表:
非常满意 | 满意 | 合计 | |
| 30 |
| |
|
|
| |
合计 |
已知在被调查的100名观众中随机抽取1名,该观众是![]() 地区当中“非常满意”的观众的概率为
地区当中“非常满意”的观众的概率为![]() ,且
,且![]() .
.
(Ⅰ)现从100名观众中用分层抽样的方法抽取20名进行问卷调查,则应抽取“满意”的![]() 、
、![]() 地区的人数各是多少;
地区的人数各是多少;
(Ⅱ)完成上述表格,并根据表格判断是否有![]() 的把握认为观众的满意程度与所在地区有关系;
的把握认为观众的满意程度与所在地区有关系;
(Ⅲ)若以抽样调查的频率为概率,从![]() 地区随机抽取3人,设抽到的观众“非常满意”的人数为
地区随机抽取3人,设抽到的观众“非常满意”的人数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
|
|
|
|
|
|
|
|
|
|
附:参考公式:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了更好地规划进货的数量,保证蔬菜的新鲜程度,某蔬菜商店从某一年的销售数据中,随机抽取了8组数据作为研究对象,如表所示(![]() (吨)为买进蔬菜的数量,
(吨)为买进蔬菜的数量,![]() (天)为销售天数):
(天)为销售天数):
| 2 | 3 | 4 | 5 | 6 | 7 | 9 | 12 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
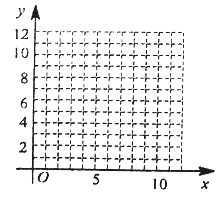
(1)根据上表数据在所给坐标系中绘制散点图,并用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据(Ⅰ)中的计算结果,该蔬菜商店准备一次性买进25吨,预计需要销售多少天?
(参考数据和公式:![]() ,
,![]() ,
,![]() ,
,![]() ,
,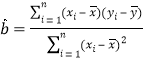
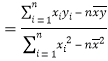 ,
,![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙、丁四位同学高考之后计划去![]() 三个不同社区进行帮扶活动,每人只能去一个社区,每个社区至少一人.其中甲必须去
三个不同社区进行帮扶活动,每人只能去一个社区,每个社区至少一人.其中甲必须去![]() 社区,乙不去
社区,乙不去![]() 社区,则不同的安排方法种数为 ( )
社区,则不同的安排方法种数为 ( )
A. 24 B. 8 C. 7 D. 6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2015年推出一种新型家用轿车,购买时费用为16.9万元,每年应交付保险费、养路费及汽油费共1.2万元,汽车的维修费为:第一年无维修费用,第二年为0.2万元,从第三年起,每年的维修费均比上一年增加0.2万元.
(I)设该辆轿车使用n年的总费用(包括购买费用、保险费、养路费、汽油费及维修费)为f(n),求f(n)的表达式;
(II)这种汽车使用多少报废最合算(即该车使用多少年,年平均费用最少)?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com