
����Ŀ���Ϻ������벨����˾2018��2���ڹ���ǩ��Э�飬˫�������ĿĻ���Ŀ�仧���ݿո۾�����������Э�飬˫������ά����ת�á�֧����Ŀ��������ѵ�ȷ��濪չս�Ժ���������֯�߶���ļ��100������־Ը����ѵ����֯һ��֪ʶ�����������óɼ��Ƴ�����Ƶ�ʷֲ�ֱ��ͼ���ٶ�ÿ���������ڵijɼ����ȷֲ�������֯�ƻ��Գɼ�ǰ20���IJ����߽��н�����

��1�������ܽ����ķ����ߣ�
��2�����ܽ�����20�������÷ֲ������ȡ5�ˣ��ٴӳ�ȡ��5���г�ȡ2�������᳡��������2�˳ɼ�����90�����ϣ���90�֣��ĸ���.
���𰸡�(1) ![]() .
.
(2) ![]() .
.
��������������������Ƶ�ʷֲ�ֱ��ͼ֪�������ɼ�����![]() ��
��![]() �ֵ����������ܽ���������Ϊ
�ֵ����������ܽ���������Ϊ![]() ���г����̼�����⣻
���г����̼�����⣻
�����ɣ���֪�����÷ֲ��������֪������![]() �ij�ȡ2�ˣ�������
�ij�ȡ2�ˣ�������![]() �ij�ȡ3�ˣ��������
�ij�ȡ3�ˣ��������![]() ��2�˷ֱ�Ϊ
��2�˷ֱ�Ϊ![]() ��������
��������![]() ��3�˷ֱ�Ϊ
��3�˷ֱ�Ϊ![]() �����ùŵ���ͼ�����ʵļ��㹫ʽ��������⣮
�����ùŵ���ͼ�����ʵļ��㹫ʽ��������⣮
��⣺������Ƶ�ʷֲ�ֱ��ͼ֪�������ɼ���![]() �ֵ�����Ϊ
�ֵ�����Ϊ![]() ��
��
�����ɼ���![]() ������Ϊ
������Ϊ![]() ��
��
���ܽ�����������![]() ֮�䣬
֮�䣬
���ܽ���������Ϊ![]() ����
����![]() ��
��
���![]() �����ܽ���������Ϊ
�����ܽ���������Ϊ![]() ��
��
�����ɣ���֪���ܽ�����20���У�������![]() ������Ϊ8��������
������Ϊ8��������![]() ������Ϊ12��
������Ϊ12��
���÷ֲ��������֪������![]() �ij�ȡ2�ˣ�������
�ij�ȡ2�ˣ�������![]() �ij�ȡ3�ˣ�
�ij�ȡ3�ˣ�
�������![]() ��2�˷ֱ�Ϊ
��2�˷ֱ�Ϊ![]() ��������
��������![]() ��3�˷ֱ�Ϊ
��3�˷ֱ�Ϊ![]() ��
��
���еĿ��������![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �����������������
�����������������![]() ��
��![]() ��
��![]() ������ĸ���Ϊ
������ĸ���Ϊ![]() ��
��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��![]() ��
��![]() ��
��![]() ��
��![]() �ļ���Ʒ�μӺ�ģ����Ʒ����.��֪���ļ���Ʒ��ǡ��������.�ڽ������ǰ���ס��ҡ���������λͬѧ�����ļ�������Ʒ�Ļ����Ԥ�����£�
�ļ���Ʒ�μӺ�ģ����Ʒ����.��֪���ļ���Ʒ��ǡ��������.�ڽ������ǰ���ס��ҡ���������λͬѧ�����ļ�������Ʒ�Ļ����Ԥ�����£�
��˵����![]() ��
��![]() ͬʱ����
ͬʱ����
��˵����![]() ��
��![]() ������ͬʱ����
������ͬʱ����
��˵����![]() ����
����
��˵����![]() ��
��![]() ����һ����.
����һ����.
���������λͬѧ������ֻ�ж�λͬѧ��Ԥ������ȷ�ģ������Ʒ�ǣ� ��
A. ��Ʒ![]() ����Ʒ
����Ʒ![]() B. ��Ʒ
B. ��Ʒ![]() ����Ʒ
����Ʒ![]() C. ��Ʒ
C. ��Ʒ![]() ����Ʒ
����Ʒ![]() D. ��Ʒ
D. ��Ʒ![]() ����Ʒ
����Ʒ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() ��,��֪
��,��֪![]() ��
��![]() ��
��![]() �ϣ���
�ϣ���![]() ����
����![]() ƽ��
ƽ��![]() .
.

������֤��![]() ƽ��
ƽ��![]() ��
��
����������![]() ������ֵ��
������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ��ֱ��l��
��ֱ��l��![]() ����ԲC�İ뾶Ϊ1��Բ����l�ϣ�
����ԲC�İ뾶Ϊ1��Բ����l�ϣ�
![]() ��Բ��CҲ��ֱ��
��Բ��CҲ��ֱ��![]() �ϣ���A��ԲC�����ߣ������߷��̣�
�ϣ���A��ԲC�����ߣ������߷��̣�
![]() ��ԲC�ϴ��ڵ�M��ʹ
��ԲC�ϴ��ڵ�M��ʹ![]() ����Բ��C�ĺ�����aȡֵ��Χ��
����Բ��C�ĺ�����aȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() �У�
��![]() ����
����![]() ,
,![]() ,
,![]() ��
��![]() ��
��![]() ���е㣬
���е㣬![]() ���߶�
���߶�![]() �ϵ�һ�㣬��
�ϵ�һ�㣬��![]() ������
������![]() .
.
��l����֤��![]() ƽ��
ƽ��![]() ��
��
��2����ֱ��![]() ��ƽ��
��ƽ��![]() ���ɽǵ�����ֵ��
���ɽǵ�����ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ʒ�Ĺ�����x�����۶�y��ͳ�����������
������x����Ԫ�� | 1 | 2 | 4 | 5 |
���۶�y����Ԫ�� | 6 | 14 | 28 | 32 |
�����ϱ��е����ݿ���������Իع鷽�� ![]() =
= ![]() x+
x+ ![]() �е�
�е� ![]() Ϊ6.6���ݴ�ģ��Ԥ��������Ϊ10��Ԫʱ���۶�Ϊ�� ��
Ϊ6.6���ݴ�ģ��Ԥ��������Ϊ10��Ԫʱ���۶�Ϊ�� ��
A.66.2��Ԫ
B.66.4��Ԫ
C.66.8��Ԫ
D.67.6��Ԫ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�о�ijҩƷ����Ч��ѡȡ������־Ը�߽����ٴ����飬����־Ը�ߵ�����ѹ���ݣ���λ��![]() ���ķ�������Ϊ
���ķ�������Ϊ![]() ��
��![]() ��
��![]() ��
��![]() ��
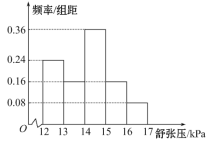
��![]() �����䰴�����ҵ�˳��ֱ���Ϊ��һ�飬�ڶ��飬......��������.��ͼ�Ǹ������������Ƴɵ�Ƶ�ʷֲ�ֱ��ͼ.��֪��һ����ڶ��鹲��
�����䰴�����ҵ�˳��ֱ���Ϊ��һ�飬�ڶ��飬......��������.��ͼ�Ǹ������������Ƴɵ�Ƶ�ʷֲ�ֱ��ͼ.��֪��һ����ڶ��鹲��![]() �ˣ���������û����Ч����
�ˣ���������û����Ч����![]() �ˣ��������������Ч������Ϊ( )
�ˣ��������������Ч������Ϊ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
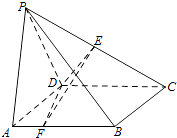
����Ŀ����ͼ��������P��ABCD�У�����ABCD�������Σ�AD=PD=2��PA=2 ![]() ����PDC=120�㣬��EΪ�߶�PC���е㣬��F���߶�AB�ϣ� ������AF=
����PDC=120�㣬��EΪ�߶�PC���е㣬��F���߶�AB�ϣ� ������AF= ![]() ����֤��CD��EF��
����֤��CD��EF��
������ƽ��DEF��ƽ��DPA���ɶ���ǵ�ƽ���Ϊ�ȣ���ȷ����F��λ�ã�ʹ��cos��= ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲����е�ʽ��12=1��12��22=��3��12��22+32=6��12��22+32��42=��10���������ϵ�ʽ�Ʋһ��һ��Ľ��ۣ�����n��N* �� 12��22+32��42+��+����1��n+1n2= ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com