
如图,AB是圆的直径,PA垂直圆所在的平面,C是圆周上的一点.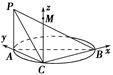
(1)求证:平面PAC⊥平面PBC;(6分)
(2)若AB=2,AC=1,PA=1,求二面角CPBA的余弦值.(6分)
(1)答案见详解;(2)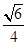
解析试题分析:(1)通过线面垂直即BC⊥平面PAC,可得平面PAC⊥平面PBC;(2)建立空间坐标系,求出两平面的法向量求解或利用线面垂直性质,做出二面角平面角,再求解.
试题解析:(1)证明 由AB是圆的直径,得AC⊥BC,
由PA⊥平面ABC,BC?平面ABC,得PA⊥BC.
又PA∩AC=A,PA?平面PAC,AC?平面PAC,
所以BC⊥平面PAC.
因为BC?平面PBC,
所以平面PBC⊥平面PAC.(5分)
(2)解 方法一 过C作CM∥AP,则CM⊥平面ABC.
如图,以点C为坐标原点,分别以直线CB、CA、CM为x轴,y轴,z轴建立空间直角坐标系.
因为AB=2,AC=1,所以BC= .
.
因为PA=1,所以A(0,1,0),B( ,0,0),P(0,1,1).
,0,0),P(0,1,1).
故C =(
=( ,0,0),C
,0,0),C =(0,1,1).
=(0,1,1).
设平面BCP的法向量为n1=(x,y,z),则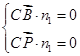 所以
所以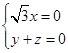
不妨令y=1,则n1=(0,1,-1).
因为A =(0,0,1),A
=(0,0,1),A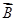 =(
=( ,-1,0),
,-1,0),
设平面ABP的法向量为n2=(x,y,z),
则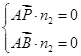
所以
不妨令x=1,则n2=(1, ,0).
,0).
于是cos〈n1,n2〉=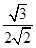 =
=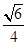 .
.
所以由题意可知二面角CPBA的余弦值为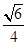 .(10分)
.(10分)
方法二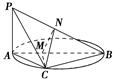
过C作CM⊥AB于M,因为PA⊥平面ABC,CM?平面ABC,
所以PA⊥CM,又PA∩AB=A,故CM⊥平面PAB.
过M作MN⊥PB于N,连接NC,
由三垂线定理得CN⊥PB,
所以∠CNM为二面角CPBA的平面角.
在Rt△ABC中,由AB=2,AC=1,
得BC= ,CM=
,CM=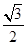 ,BM=
,BM=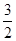 ,
,
在R t△PAB中,由AB=2,PA=1,得PB=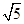 .
.
因为Rt△BNM∽Rt△BAP,
所以=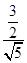 ,故MN=
,故MN=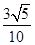 .
.
又在Rt△CNM中,CN=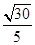 ,故cos∠CNM=
,故cos∠CNM=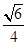 .
.
所以二面角CPBA的余弦值为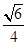 .(10分)
.(10分)
考点:1、面面垂直;2、二面角.


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源: 题型:解答题
如图所示, 平面
平面 ,四边形
,四边形 是矩形,
是矩形,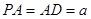 ,M,N分别是AB,PC的中点,
,M,N分别是AB,PC的中点,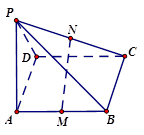
(1)求平面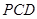 和平面
和平面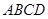 所成二面角的大小,
所成二面角的大小,
(2)求证: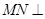 平面
平面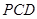
(3)当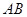 的长度变化时,求异面直线PC与AD所成角的可能范围.
的长度变化时,求异面直线PC与AD所成角的可能范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图示,在底面为直角梯形的四棱椎P ABCD中,AD//BC,ÐABC= 900, PA^平面ABCD,PA= 4,AD= 2,AB=2 ,BC = 6.
,BC = 6.
(1)求证:BD^平面PAC ;
(2)求二面角A—PC—D的正切值;
(3)求点D到平面PBC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,AC 是圆 O 的直径,点 B 在圆 O 上,∠BAC=30°,BM⊥AC交 AC 于点 M,EA⊥平面ABC,FC//EA,AC=4,EA=3,FC=1.
(I)证明:EM⊥BF;
(II)求平面 BEF 与平面ABC 所成锐二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com