
【题目】已知函数![]() .
.
(1)当![]() 时,证明
时,证明![]() 的图象与
的图象与![]() 轴相切;
轴相切;
(2)当![]() 时,证明
时,证明![]() 存在两个零点.
存在两个零点.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)先求导,再设切点,求出切点坐标,即可证明,
(2)分离参数,构造函数,利用导数求出函数的最值,即可证明.
证明:(1)当a=1时,f(x)=(x﹣2)lnx+x﹣1.
∴f′(x)=lnx+![]() +1,
+1,
若f(x)与x轴相切,切点为(x0,0),
∴f(x0)=(x0﹣2)lnx0+x0﹣1=0
f′(x0)=lnx0+![]() +1=0,
+1=0,
解得x0=1或x0=4(舍去)
∴x0=1,
∴切点为(1,0),
故f(x)的图象与x轴相切
(2)∵f(x)=(x﹣2)lnx+ax﹣1=0,
∴a=![]() ﹣
﹣![]() =
=![]() ﹣lnx+
﹣lnx+![]() ,
,
设g(x)=![]() ﹣lnx+
﹣lnx+![]() ,
,
∴g′(x)=﹣![]() ﹣
﹣![]() +
+![]() =
=![]() ,
,
令h(x)=1﹣2x﹣2lnx
易知h(x)在(0,+∞)为减函数,
∵h(1)=1﹣1﹣2ln1=0,
∴当x∈(0,1)时,g′(x)>0,函数g(x)单调递增,
当x∈(1,+∞)时,g′(x)<0,函数g(x)单调递减,
∴g(x)max=g(1)=1,
当x→0时,g(x)→﹣∞,当x→+∞时,g(x)→﹣∞,
∴当a<1时,y=g(x)与y=a有两个交点,
即当a<1时,证明f(x)存在两个零点


科目:高中数学 来源: 题型:
【题目】如图,在几何体![]() 中,底面
中,底面![]() 为矩形,
为矩形,![]() ,
,![]() ,
,![]() ,
,![]() .
.![]() 为棱
为棱![]() 上一点,平面
上一点,平面![]() 与棱
与棱![]() 交于点
交于点![]() .
.
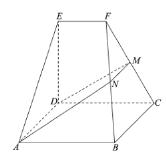
(1)求证:![]() ;
;
(2)若![]() ,试问平面
,试问平面![]() 是否可能与平面
是否可能与平面![]() 垂直?若能,求出
垂直?若能,求出![]() 的值;若不能,说明理由.
的值;若不能,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣a|+|x+2|.
(1)当a=1 时,求不等式f(x)≤5的解集;
(2)x0∈R,f(x0)≤|2a+1|,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 分别为
分别为![]() 的三内角A,B,C的对边,其面积
的三内角A,B,C的对边,其面积![]() ,在等差数列
,在等差数列![]() 中,
中,![]() ,公差
,公差![]() .数列
.数列![]() 的前n项和为
的前n项和为![]() ,且
,且![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】追求人类与生存环境的和谐发展是中国特色社会主义生态文明的价值取向.为了改善空气质量,某城市环保局随机抽取了一年内100天的空气质量指数(![]() )的检测数据,结果统计如下:
)的检测数据,结果统计如下:
|
|
|
|
|
|
|
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
天数 | 6 | 14 | 18 | 27 | 25 | 10 |
(1)从空气质量指数属于![]() ,
,![]() 的天数中任取3天,求这3天中空气质量至少有2天为优的概率;
的天数中任取3天,求这3天中空气质量至少有2天为优的概率;
(2)已知某企业每天的经济损失![]() (单位:元)与空气质量指数
(单位:元)与空气质量指数![]() 的关系式为
的关系式为 ,试估计该企业一个月(按30天计算)的经济损失的数学期望.
,试估计该企业一个月(按30天计算)的经济损失的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),其中
为参数),其中![]() .以坐标原点为极点,
.以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,与
,与![]() 交于
交于![]() 两点,且
两点,且![]() ,求
,求![]() 的普通方程.
的普通方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com