
【题目】已知函数![]() ,函数
,函数![]() (
(![]() ).
).
(1)讨论![]() 的单调性;
的单调性;
(2)证明:当![]() 时,
时,![]() .
.
(3)证明:当![]() 时,
时,![]() .
.
科目:高中数学 来源: 题型:
【题目】某中学2018年的高考考生人数是2015年高考考生人数的![]() 倍,为了更好地对比该校考生的升学情况,统计了该校2015年和2018年的高考情况,得到如图柱状图:
倍,为了更好地对比该校考生的升学情况,统计了该校2015年和2018年的高考情况,得到如图柱状图:

则下列结论正确的是![]()
![]()
A. 与2015年相比,2018年一本达线人数减少
B. 与2015年相比,2018年二本达线人数增加了![]() 倍
倍
C. 2015年与2018年艺体达线人数相同
D. 与2015年相比,2018年不上线的人数有所增加
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 内,动点
内,动点![]() 到定点
到定点![]() 的距离与
的距离与![]() 到定直线
到定直线![]() 距离之比为
距离之比为![]() .
.
(Ⅰ)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)设点![]() 是轨迹
是轨迹![]() 上两个动点直线
上两个动点直线![]() 与轨迹
与轨迹![]() 的另一交点分别为
的另一交点分别为![]() 且直线
且直线![]() 的斜率之积等于
的斜率之积等于![]() ,问四边形
,问四边形![]() 的面积
的面积![]() 是否为定值?请说明理由.
是否为定值?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列{an}的前n项和为Sn,已知:a5=2a2+3且a2,![]() ,a14成等比数列.
,a14成等比数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设正项数列{bn}满足bn2Sn+1=Sn+1+2,求证:b1+b2+…+bn<n+1.
查看答案和解析>>
科目:高中数学 来源: 题型:
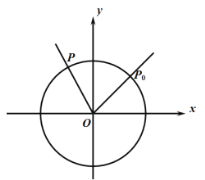
【题目】如图,单位圆上有一点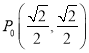 ,点
,点![]() 以点
以点![]() 为起点按逆时针方向以每秒
为起点按逆时针方向以每秒![]() 弧度作圆周运动,点
弧度作圆周运动,点![]() 的纵坐标
的纵坐标![]() 是关于时间
是关于时间![]() 的函数,记作
的函数,记作![]() .
.
(1)当![]() 时,求
时,求![]() ;
;
(2)若将函数![]() 向左平移
向左平移![]() 个单位长度后,得到的曲线关于
个单位长度后,得到的曲线关于![]() 轴对称,求
轴对称,求![]() 的最小正值,并求此时
的最小正值,并求此时![]() 在
在![]() 的值域.
的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学棋艺协会定期举办“以棋会友”的竞赛活动,分别包括“中国象棋”、“围棋”、“五子棋”、“国际象棋”四种比赛,每位协会会员必须参加其中的两种棋类比赛,且各队员之间参加比赛相互独立;已知甲同学必选“中国象棋”,不选“国际象棋”,乙同学从四种比赛中任选两种参与.
(1)求甲参加围棋比赛的概率;
(2)求甲、乙两人参与的两种比赛都不同的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC—A1B1C1中,AA1=AC,A1B⊥AC1,设O为AC1与A1C的交点,点P为BC的中点.求证:
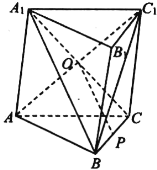
(1)OP∥平面ABB1A1;
(2)平面ACC1⊥平面OCP.
查看答案和解析>>
科目:高中数学 来源: 题型:
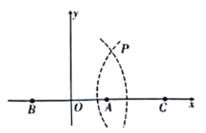
【题目】双曲线定位法是通过测定待定点到至少三个已知点的两个距离差所进行的一种无线电定位.通过船(待定点)接收到三个发射台的电磁波的时间差计算出距离差,两个距离差即可形成两条位置双曲线,两者相交便可确定船位.我们来看一种简单的“特殊”状况;如图所示,已知三个发射台分别为![]() ,
,![]() ,
,![]() 且刚好三点共线,已知
且刚好三点共线,已知![]() 海里,
海里,![]() 海里,现以
海里,现以![]() 的中点为原点,
的中点为原点,![]() 所在直线为
所在直线为![]() 轴建系.现根据船
轴建系.现根据船![]() 接收到
接收到![]() 点与
点与![]() 点发出的电磁波的时间差计算出距离差,得知船
点发出的电磁波的时间差计算出距离差,得知船![]() 在双曲线
在双曲线![]() 的左支上,若船
的左支上,若船![]() 上接到
上接到![]() 台发射的电磁波比
台发射的电磁波比![]() 台电磁波早
台电磁波早![]() (已知电磁波在空气中的传播速度约为
(已知电磁波在空气中的传播速度约为![]() ,1海里
,1海里![]() ),则点
),则点![]() 的坐标(单位:海里)为( )
的坐标(单位:海里)为( )
A. B.
B.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com