
【题目】某大学棋艺协会定期举办“以棋会友”的竞赛活动,分别包括“中国象棋”、“围棋”、“五子棋”、“国际象棋”四种比赛,每位协会会员必须参加其中的两种棋类比赛,且各队员之间参加比赛相互独立;已知甲同学必选“中国象棋”,不选“国际象棋”,乙同学从四种比赛中任选两种参与.
(1)求甲参加围棋比赛的概率;
(2)求甲、乙两人参与的两种比赛都不同的概率.
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:高中数学 来源: 题型:
【题目】某校在一次期末数学测试中,为统计学生的考试情况,从学校的2000名学生中随机抽取50名学生的考试成绩,被测学生成绩全部介于65分到145分之间(满分150分),将统计结果按如下方式分成八组:第一组![]() ,
,![]() ,第二组
,第二组![]() ,
,![]() ,
,![]() 第八组
第八组![]() ,
,![]() ,如图是按上述分组方法得到的频率分布直方图的一部分.
,如图是按上述分组方法得到的频率分布直方图的一部分.
(1)求第七组的频率,并完成频率分布直方图;
(2)用样本数据估计该校的2000名学生这次考试成绩的平均分(同一组中的数据用该组区间的中点值代表该组数据平均值);
(3)若从样本成绩属于第六组和第八组的所有学生中随机抽取2名,求他们的分差的绝对值小于10分的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系![]() 中,曲线
中,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() ,设
,设![]() 与
与![]() 交于
交于![]() 、
、![]() 两点,
两点,![]() 中点为
中点为![]() ,
,![]() 的垂直平分线交
的垂直平分线交![]() 于
于![]() 、
、![]() .以
.以![]() 为坐标原点,极轴为
为坐标原点,极轴为![]() 轴的正半轴建立直角坐标系
轴的正半轴建立直角坐标系![]() .
.
(1)求![]() 的直角坐标方程与点
的直角坐标方程与点![]() 的直角坐标;
的直角坐标;
(2)求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设经过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() 、
、![]() 两点,经过点
两点,经过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 相切于点
相切于点![]() .
.
(1)当![]() 时,求
时,求![]() 的取值范围;
的取值范围;
(2)问是否存在直线![]() ,
,![]() 使得
使得![]() 成立,若存在,求出
成立,若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,已知![]() ,顶点P在平面ABC上的射影为
,顶点P在平面ABC上的射影为![]() 的外接圆圆心.
的外接圆圆心.
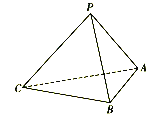
(1)证明:平面![]() 平面ABC;
平面ABC;
(2)若点M在棱PA上,![]() ,且二面角P-BC-M的余弦值为
,且二面角P-BC-M的余弦值为![]() ,试求
,试求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某印刷厂为了研究单册书籍的成本![]() (单位:元)与印刷册数
(单位:元)与印刷册数![]() (单位:千册)之间的关系,在印制某种书籍时进行了统计,相关数据见下表:
(单位:千册)之间的关系,在印制某种书籍时进行了统计,相关数据见下表:
印刷册数 |
|
|
|
|
|
单册成本 |
|
|
|
|
|
根据以上数据,技术人员分别借助甲、乙两种不同的回归模型,得到两个回归方程,方程甲:![]() ,方程乙:
,方程乙:![]() .
.
(1)为了评价两种模型的拟合效果,完成以下任务.
①完成下表(计算结果精确到![]() );
);
印刷册数 |
|
|
|
|
| |
单册成本 |
|
|
|
|
| |
模型甲 | 估计值 |
|
|
| ||
残差 |
|
|
| |||
模型乙 | 估计值 |
|
|
| ||
残差 |
|
|
| |||
②分别计算模型甲与模型乙的残差平方和,并通过比较,判断哪个模型拟合效果更好.
(2)该书上市之后,受到广大读者热烈欢迎,不久便全部售罄,于是印刷厂决定进行二次印刷,根据市场调查,新需求量为![]() 千册,若印刷厂以每册
千册,若印刷厂以每册![]() 元的价格将书籍出售给订货商,求印刷厂二次印刷
元的价格将书籍出售给订货商,求印刷厂二次印刷![]() 千册获得的利润?(按(1)中拟合效果较好的模型计算印刷单册书的成本).
千册获得的利润?(按(1)中拟合效果较好的模型计算印刷单册书的成本).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】概率论起源于博弈游戏.17世纪,曾有一个“赌金分配“的问题:博弈水平相当的甲、乙两人进行博弈游戏,每局比赛都能分出胜负,没有平局.双方约定,各出赌金48枚金币,先赢3局者可获得全部赌金;但比赛中途因故终止了,此时甲赢了2局,乙赢了1局.向这96枚金币的赌金该如何分配?数学家费马和帕斯卡都用了现在称之为“概率“的知识,合理地给出了赌金分配方案.该分配方案是( )
A.甲48枚,乙48枚B.甲64枚,乙32枚
C.甲72枚,乙24枚D.甲80枚,乙16枚
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com