
如图,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,M为EC的中点,AF=AB=BC=FE=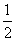 AD.
AD.
(1)求异面直线BF与DE所成的角的大小;
(2)证明平面AMD⊥平面CDE;
(2)求二面角ACDE的余弦值.
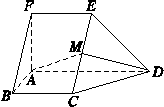
解 如图所示,建立空间直角坐标系,点A为坐标原
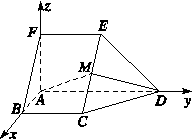 点.
点.
设AB=1,依题意得B(1,0,0),
C(1,1,0),D(0,2,0),E(0,1,1),F(0,0,1),
M(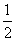 ,1,
,1,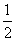 ).
).
(1) 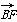 =(-1,0,1),
=(-1,0,1),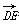 =(0,-1,1),
=(0,-1,1),
于是cos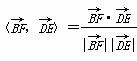 =
= =
=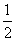 .
.
所以异面直线BF与DE所成的角的大小为60°.
(2)证明 由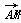 =(
=(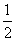 ,1,
,1,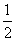 ),
),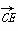 =(-1,0,1),
=(-1,0,1),
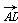 =(0,2,0),可得
=(0,2,0),可得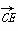 ·
·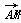 =0,
=0,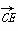 ·
·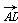 =0.
=0.
因此,CE⊥AM,CE⊥AD.
又AM∩AD=A,故CE⊥平面AMD.
而CE⊂平面CDE,所以平面AMD⊥平面CDE.
(3)设平面CDE的法向量为u=(x,y,z),
则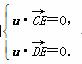
于是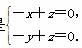 令x=1,可得u=(1,1,1).
令x=1,可得u=(1,1,1).
又由题设,平面ACD的一个法向量为v=(0,0,1).
所以,cos〈u,v〉=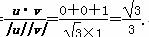
因为二面角ACDE为锐角,所以其余弦值为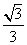 .
.


科目:高中数学 来源: 题型:
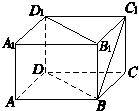
如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,则BC1与平面BB1D1D所成角的正弦值为 ( ).
A.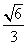 B.
B.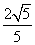
C. D.
D.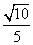
查看答案和解析>>
科目:高中数学 来源: 题型:
给出下列结论:
①若命题p:∃x∈R,tan x=1;命题q:∀x∈R,x2-x+1>0,则命题“p∧綈q”是假命题;
②已知直线l1:ax+3y-1=0,l2:x+by+1=0,则l1⊥l2的充要条件是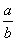 =-3;
=-3;
③命题“若x2-3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0”.
其中正确结论的序号为________(把你认为正确的结论的序号都填上).
查看答案和解析>>
科目:高中数学 来源: 题型:
函数y=sin(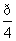 -2x)的单调增区间是 ( )
-2x)的单调增区间是 ( )
A. [kπ-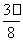 , kπ+
, kπ+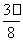 ] (k∈Z) B. [kπ+
] (k∈Z) B. [kπ+ ,
,  kπ+
kπ+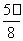 ] (k∈Z)
] (k∈Z)
C. [kπ- , kπ+
, kπ+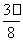 ] (k∈Z) D. [kπ+
] (k∈Z) D. [kπ+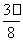 , kπ+
, kπ+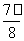 ] (k∈Z)
] (k∈Z)
查看答案和解析>>
科目:高中数学 来源: 题型:
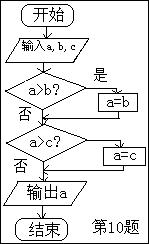
给出以下一个算法的程序框图(如图所示),该程序框图的功能是( )
A.求输出a,b,c三数的最大数
B.求输出a,b,c三数的最小数
C.将a,b,c按从小到大排列
D.将a,b,c按从大到小排列
查看答案和解析>>
科目:高中数学 来源: 题型:
对一批产品的长度(单位:毫米)进行抽样检测,下图为检测结果的频率分布直方图.根据标准,产品长度在区间[20,25)上为一等品,在区间[15,20)和[25,30)上为二等品,在区间[10,15)和[30,35]上为三 等品.用频率估计概率,现从该批产品中随机抽取1件,则其为二等品的概率是( )
等品.用频率估计概率,现从该批产品中随机抽取1件,则其为二等品的概率是( )
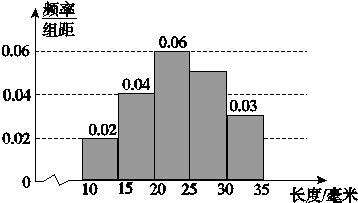
A.0.09 B.0.20
C.0.25 D.0.45
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com