
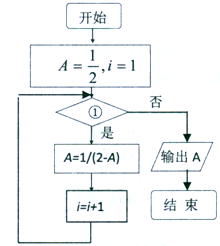
 如图所示的程序框图,若执行后的结果是$\frac{5}{6}$,则在①处应填写的是( )
如图所示的程序框图,若执行后的结果是$\frac{5}{6}$,则在①处应填写的是( )| A. | i≤3 | B. | i≤4 | C. | i≤5 | D. | i≤6 |
分析 根据条件,进行模拟运行,找到满足输出结果为$\frac{5}{6}$的条件即可.
解答 解:第一次循环,i=1,满足条件,A=$\frac{1}{2-\frac{1}{2}}=\frac{1}{\frac{3}{2}}$=$\frac{2}{3}$,i=2,
第二次循环,i=2,满足条件,A=$\frac{1}{2-\frac{2}{3}}=\frac{1}{\frac{4}{3}}=\frac{3}{4}$,i=3,
第三次循环,i=3,满足条件,A=$\frac{1}{2-\frac{3}{4}}=\frac{1}{\frac{5}{4}}=\frac{4}{5}$,i=4,
第四次循环,i=4,满足条件,A=$\frac{1}{2-\frac{4}{5}}=\frac{1}{\frac{6}{5}}$=$\frac{5}{6}$,i=5,
此时i=5,不满足条件,程序终止,输出A=$\frac{5}{6}$,
即当i=1,2,3,4时,满足条件,当i=5时,不满足条件.
则条件应该为i≤4,
故选:B
点评 本题主要考查程序框图的识别和判断,根据程序条件进行模拟是解决本题的关键.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
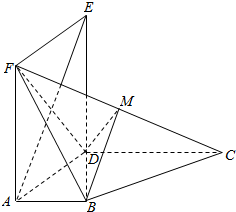 如图所示,平面ADEF⊥平面ABCD,且四边形ADEF为正方形,AD⊥DC,AB∥CD,AB=AD=$\frac{1}{2}$DC=2,M为CE的中点.
如图所示,平面ADEF⊥平面ABCD,且四边形ADEF为正方形,AD⊥DC,AB∥CD,AB=AD=$\frac{1}{2}$DC=2,M为CE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD的底面ABCD是平行四边形,M、N分别是AB、PC的中点,且MN⊥PC,MN⊥AB.证明:平面PAD⊥平面PDC.
如图,四棱锥P-ABCD的底面ABCD是平行四边形,M、N分别是AB、PC的中点,且MN⊥PC,MN⊥AB.证明:平面PAD⊥平面PDC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
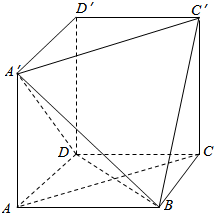 在长方体ABCD-A′B′C′D′中,AB=BC=2,过A′,C′,B三点的平面截去长方体的一个角后,得到ABCD-A′C′D′,
在长方体ABCD-A′B′C′D′中,AB=BC=2,过A′,C′,B三点的平面截去长方体的一个角后,得到ABCD-A′C′D′,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com