
分析 利用“$\frac{a}{b+c}$<$\frac{a+a}{b+c+a}$”放缩可知$\frac{a}{b+c}$<$\frac{2a}{a+b+c}$、$\frac{b}{c+a}$<$\frac{2b}{a+b+c}$、$\frac{c}{a+b}$<$\frac{2c}{a+b+c}$,相加计算即得结论.
解答 证明:依题意易知$\frac{c}{a+b}$、$\frac{a}{b+c}$、$\frac{b}{c+a}$均为正分数,
∴$\frac{a}{b+c}$<$\frac{a+a}{b+c+a}$=$\frac{2a}{a+b+c}$,
同理可知$\frac{b}{c+a}$<$\frac{2b}{a+b+c}$,$\frac{c}{a+b}$<$\frac{2c}{a+b+c}$,
∴$\frac{c}{a+b}$+$\frac{a}{b+c}$+$\frac{b}{c+a}$<$\frac{2c}{a+b+c}$+$\frac{2a}{a+b+c}$+$\frac{2b}{a+b+c}$
=$\frac{2(a+b+c)}{a+b+c}$
=2.
点评 本题考查不等式的证明,利用不等式的性质是解决本题的关键,注意解题方法的积累,属于中档题.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“p或q”为假 | B. | 命题“p且q“为真 | ||
| C. | 命题,“¬p或q”为假 | D. | 命题“p且¬q“为假 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
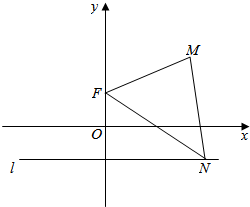 如图,已知点F(0,p),直线l:y=-p(其中p为常数,且p>0),M为平面内的动点,过M作l的垂线,垂足为N,且$\overrightarrow{NM}•\overrightarrow{NF}$=$\overrightarrow{FM}•\overrightarrow{FN}$.
如图,已知点F(0,p),直线l:y=-p(其中p为常数,且p>0),M为平面内的动点,过M作l的垂线,垂足为N,且$\overrightarrow{NM}•\overrightarrow{NF}$=$\overrightarrow{FM}•\overrightarrow{FN}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com