
分析 由已知条件得a1=1,a2=2,由已知条件得数列{an}的奇数列、偶数列分别成等比数列,由此能求出S2012.
解答 解:∵数列{an}满足a1=1,an•an+1=2n,n∈N*
∴n=1时,a2=2,
∵an•an+1=2n,∴n≥2时,an•an-1=2n-1,
∴$\frac{{a}_{n+1}}{{a}_{n-1}}$=2,
∴数列{an}的奇数列、偶数列分别成等比数列,
∴S2012=$\frac{1-{2}^{1006}}{1-2}$+$\frac{2(1-{2}^{1006})}{1-2}$=3×21006-3.
故答案为:3×21006-3.
点评 本题考查数列的前2012项的和的求法,解题时要认真审题,注意分组求和法的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
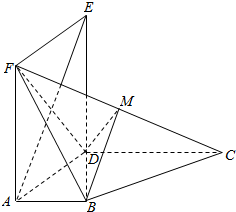 如图所示,平面ADEF⊥平面ABCD,且四边形ADEF为正方形,AD⊥DC,AB∥CD,AB=AD=$\frac{1}{2}$DC=2,M为CE的中点.
如图所示,平面ADEF⊥平面ABCD,且四边形ADEF为正方形,AD⊥DC,AB∥CD,AB=AD=$\frac{1}{2}$DC=2,M为CE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com