Question

如图，直三棱柱ABC-A₁B₁C₁中，底面是以∠ABC为直角的等腰直角三角形，AC=2a，BB₁=3a，D为A₁C₁的中点，E为B₁C的中点．

(Ⅰ)求直线BE与A₁C所成的角；

(Ⅱ)在线段AA₁上是否存在点F，使、CF⊥平面B₁DF，若存在，求出||；若不存在，说明理由．

Answer 1

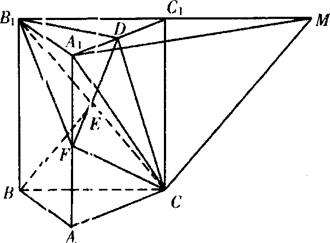
解法一：(Ⅰ)延长B₁C₁至M，连CM、A₁M则CM∥BE，

∴∠A₁CM为直线BE与AC所成的角 

∵CM=BC₁=a，A₁C=a

在△A₁C₁M中，A₁M²=(2+4+2××2×)a²=10a²

∴cos∠A₁CM=

∴直线BE与A₁C所成的角为arccos

(Ⅱ)假设存在点F，∵B₁D⊥平面A₁ACC₁，CF面A₁ACC₁，∴CF⊥B₁D 

要使CF⊥平面B₁DF，只要CF⊥B₁F．

不妨设AF=x，则A₁F=3a-x，B₁F²=(3a-x)²+2a²，

CF²=x²+4a²，B₁C²=11a²

∵CF⊥B₁F,∴B₁C²=CF²+B₁F²

∴11a²=(3a-x)²+2a²+x²+4a² 

∴x²-3ax+2a²=0    ∴x=a或x=2a

故当||=a或2a时，CF⊥平面B₁DF．

解法二：(Ⅰ)以B为原点，如图建立空间直角坐标系

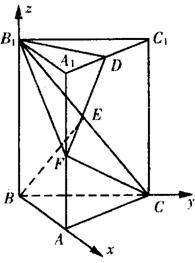
∵AC=2a，∠ABC=90°，∴AB=BC=a．

∴B(0，0，0)，C(0，a，0)，A(a,0,0)，

A₁(a,0,3a),C₁(0,a,3a),B₁(0,0,3a)．

∴D(a, a,3a),E(0, a,a)，

∴=(a,-a,3a),=(0，).

∴||=a，||=,

∴·=0-a²+a²=a².

∴cosθ=.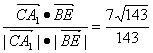

故BE与A₁C所成的角为arccos．

(Ⅱ)假设存在点F，要使CF⊥平画B₁DF，只要⊥且⊥．

不妨设AF=b，则F(a,0,b), =(a,-a,b)，

=(a，0，b-3a)，=(a，a，0)，

∵=a²-a²=0,∴恒成立．

=2a²+b(b-3a)=0b=a或b=2a,

故当||=a或2a时，CF⊥平面B₁DF．