
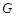 的离心率为
的离心率为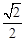 ,短轴端点分别为
,短轴端点分别为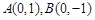 .
. 的标准方程;
的标准方程;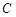 ,
,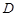 是椭圆
是椭圆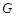 上关于
上关于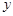 轴对称的两个不同点,直线
轴对称的两个不同点,直线 与
与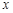 轴交于点
轴交于点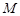 ,判断以线段
,判断以线段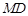 为直径的圆是否过点
为直径的圆是否过点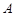 ,并说明理由.
,并说明理由.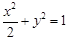 ;(2)点
;(2)点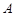 不在以线段
不在以线段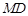 为直径的圆上.
为直径的圆上.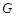 的标准方程,已知椭圆
的标准方程,已知椭圆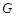 的离心率为
的离心率为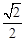 ,短轴端点分别为
,短轴端点分别为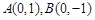 ,可设椭圆方程为
,可设椭圆方程为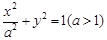 ,由
,由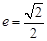 ,可得
,可得 ,从而得椭圆
,从而得椭圆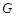 的标准方程;(2)由于
的标准方程;(2)由于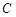 ,
,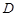 是椭圆
是椭圆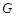 上关于
上关于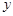 轴对称的两个不同点,可设
轴对称的两个不同点,可设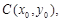 则
则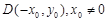 ,若点
,若点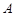 在以线段
在以线段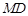 为直径的圆上,则
为直径的圆上,则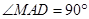 ,即
,即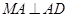 ,即
,即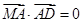 ,因此可写出直线
,因此可写出直线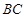 的方程为
的方程为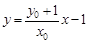 ,令
,令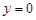 ,得
,得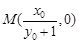 ,写出向量
,写出向量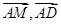 的坐标,看
的坐标,看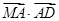 是否等于0,即可判断出.
是否等于0,即可判断出.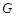 的方程为:
的方程为: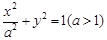 1分
1分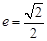 ,可得
,可得 , 3分
, 3分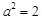 , 4分
, 4分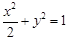 . 5分
. 5分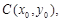 则
则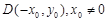 6分
6分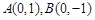 ,
,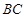 的方程为
的方程为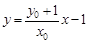 , 7分
, 7分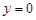 ,得
,得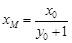 ,所以
,所以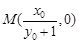 . 8分
. 8分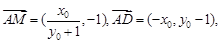 9分
9分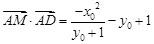 , 10分
, 10分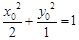 ,代入得
,代入得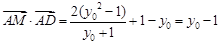 11分
11分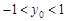 ,所以
,所以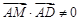 . 12分
. 12分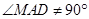 , 13分
, 13分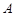 不在以线段
不在以线段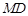 为直径的圆上. 14分
为直径的圆上. 14分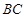 的方程为
的方程为 ,则
,则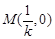 . 6分
. 6分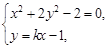 化简得到
化简得到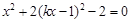 ,
,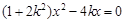 ,所以
,所以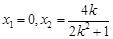 , 8分
, 8分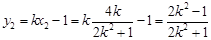 ,
,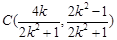 ,所以
,所以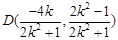 9分
9分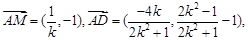 10分
10分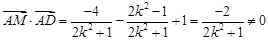 , 12分
, 12分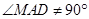 , 13分
, 13分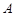 不在以线段
不在以线段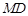 为直径的圆上. 14分
为直径的圆上. 14分

科目:高中数学 来源:不详 题型:解答题
 ,过点
,过点 任作一直线与
任作一直线与 相交于
相交于 两点,过点
两点,过点 作
作 轴的平行线与直线
轴的平行线与直线 相交于点
相交于点 (
( 为坐标原点).
为坐标原点).
 在定直线上;
在定直线上; 的任意一条切线
的任意一条切线 (不含
(不含 轴)与直线
轴)与直线 相交于点
相交于点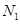 ,与(1)中的定直线相交于点
,与(1)中的定直线相交于点 ,证明:
,证明: 为定值,并求此定值.
为定值,并求此定值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 的方程为
的方程为 ,过原点作斜率为
,过原点作斜率为 的直线和曲线
的直线和曲线 相交,另一个交点记为
相交,另一个交点记为 ,过
,过 作斜率为
作斜率为 的直线与曲线
的直线与曲线 相交,另一个交点记为
相交,另一个交点记为 ,过
,过 作斜率为
作斜率为 的直线与曲线
的直线与曲线 相交,另一个交点记为
相交,另一个交点记为 ,如此下去,一般地,过点
,如此下去,一般地,过点 作斜率为
作斜率为 的直线与曲线
的直线与曲线 相交,另一个交点记为
相交,另一个交点记为 ,设点
,设点 (
( ).
). ,并求
,并求 与
与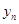 的关系式(
的关系式( );
); (
( )的通项公式,并指出点列
)的通项公式,并指出点列 ,
, ,
, ,向哪一点无限接近?说明理由;
,向哪一点无限接近?说明理由; ,数列
,数列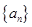 的前
的前 项和为
项和为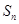 ,试比较
,试比较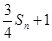 与
与 的大小,并证明你的结论.
的大小,并证明你的结论.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 的焦点为
的焦点为 ,点
,点 ,线段
,线段 的中点在抛物线上. 设动直线
的中点在抛物线上. 设动直线 与抛物线相切于点
与抛物线相切于点 ,且与抛物线的准线相交于点
,且与抛物线的准线相交于点 ,以
,以 为直径的圆记为圆
为直径的圆记为圆 .
. 的值;
的值; 与
与 轴必有公共点;
轴必有公共点;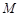 ,使得圆
,使得圆 恒过点
恒过点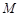 ?若存在,求出
?若存在,求出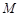 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
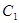 的圆心在坐标原点
的圆心在坐标原点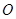 ,且恰好与直线
,且恰好与直线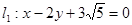 相切,设点A为圆上一动点,
相切,设点A为圆上一动点,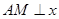 轴于点
轴于点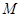 ,且动点
,且动点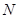 满足
满足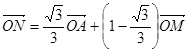 ,设动点
,设动点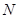 的轨迹为曲线
的轨迹为曲线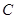
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.[2,+∞) | B.(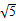 ,+∞) ,+∞) |
C.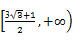 | D.(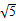 +1,+∞) +1,+∞) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 =1(a>0,b>0)的左、右焦点,过点F2作此双曲线一条渐近线的垂线,垂足为M,且满足|
=1(a>0,b>0)的左、右焦点,过点F2作此双曲线一条渐近线的垂线,垂足为M,且满足| |=3|
|=3| |,则此双曲线的渐近线方程为________.
|,则此双曲线的渐近线方程为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com