
【题目】如图,在长方体![]() 中,
中,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点,
的中点,![]() 为线段
为线段![]() 上一点,且满足
上一点,且满足![]() ,
,![]() 为
为![]() 的中点.
的中点.
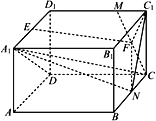
(1)求证:![]() 平面
平面![]() ;
;
(2)求三棱锥![]() 的体积;
的体积;
(3)求直线![]() 与直线
与直线![]() 所成角的余弦值.
所成角的余弦值.
【答案】(1)见解析(2)![]() (3)
(3)![]()
【解析】
(1)利用三角形的中位线和梯形的中位线的性质得到线线平行,利用面面平行的判定定理证得平面![]() 平面
平面![]() ,利用面面平行的性质得到
,利用面面平行的性质得到![]() 平面
平面![]() ;
;
(2)将三棱锥的顶点和底面转换,之后利用椎体体积公式求得结果;
(3)利用异面直线所成角的定义,得到![]() (或其补角)是目标,之后应用余弦定理求得结果.
(或其补角)是目标,之后应用余弦定理求得结果.
(1)作![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() .
.
又![]() 为
为![]() 的中点,
的中点,
∴![]() 为
为![]() 的中位线,
的中位线,![]() .
.
又![]() 为
为![]() 的中点,
的中点,
∴![]() 为梯形
为梯形![]() 的中位线,∴
的中位线,∴![]() .
.
在平面![]() 中,
中,![]() ,
,
在平面![]() 中,
中,![]() ,
,
∴平面![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
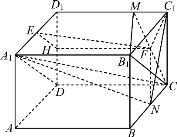
(2)![]()
![]() .
.
故所求三棱锥![]() 的体积为
的体积为![]() .
.
(3)连接![]() ,
,![]() ,因为在长方体
,因为在长方体![]() 中,
中,![]() ,
,
且![]() ,又点
,又点![]() 在直线
在直线![]() 上,
上,
所以直线![]() 与直线
与直线![]() 所成角即为
所成角即为![]() 与
与![]() 所成的角,
所成的角,
即是![]() (或其补角).
(或其补角).
在![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
由余弦定理得![]()
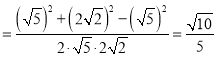 ,
,
故所求直线![]() 与直线
与直线![]() 所成角的余弦值为
所成角的余弦值为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在本题中,我们把具体如下性质的函数![]() 叫做区间
叫做区间![]() 上的闭函数:①
上的闭函数:①![]() 的定义域和值域都是
的定义域和值域都是![]() ;②
;②![]() 在
在![]() 上是增函数或者减函数.
上是增函数或者减函数.
(1)若![]() 在区间
在区间![]() 上是闭函数,求常数
上是闭函数,求常数![]() 的值;
的值;
(2)找出所有形如![]() 的函数(
的函数(![]() 都是常数),使其在区间
都是常数),使其在区间![]() 上是闭函数.
上是闭函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴为正半轴为极轴建立极坐标系.已知曲线
轴为正半轴为极轴建立极坐标系.已知曲线![]() 的极坐标方程为
的极坐标方程为![]()
![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,直线
两点,直线![]() 过定点
过定点![]() 且倾斜角为
且倾斜角为![]() 交曲线
交曲线![]() 于
于![]() 两点.
两点.
(1)把曲线![]() 化成直角坐标方程,并求
化成直角坐标方程,并求![]() 的值;
的值;
(2)若![]() 成等比数列,求直线
成等比数列,求直线![]() 的倾斜角
的倾斜角![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知多面体ABCDEF中,四边形ABFE为正方形,![]() ,
,![]() ,G为AB的中点,
,G为AB的中点,![]() .
.

(1)求证:![]() 平面CDEF;
平面CDEF;
(2)求平面ACD与平面BCF所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆C的中心在原点,左焦点![]() ,长轴为
,长轴为![]() .
.
(1)求椭圆C的标准方程;
(2)过左焦点![]() 的直线交曲线C于A,B两点,过右焦点
的直线交曲线C于A,B两点,过右焦点![]() 的直线交曲线C于C,D两点,凸四边形ABCD为菱形,求直线AB的方程.
的直线交曲线C于C,D两点,凸四边形ABCD为菱形,求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)椭圆![]()
![]() (
(![]() )的上顶点为
)的上顶点为![]() ,
, ![]() 是
是![]() 上的一点,以
上的一点,以![]() 为直径的圆经过椭圆
为直径的圆经过椭圆![]() 的右焦点
的右焦点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)动直线![]() 与椭圆
与椭圆![]() 有且只有一个公共点,问:在
有且只有一个公共点,问:在![]() 轴上是否存在两个定点,它们到直线
轴上是否存在两个定点,它们到直线![]() 的距离之积等于
的距离之积等于![]() ?如果存在,求出这两个定点的坐标;如果不存在,说明理由.
?如果存在,求出这两个定点的坐标;如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某运动制衣品牌为了成衣尺寸更精准,现选择15名志愿者,对其身高和臂展进行测量(单位:厘米),左图为选取的15名志愿者身高与臂展的折线图,右图为身高与臂展所对应的散点图,并求得其回归方程为![]() ,以下结论中不正确的为
,以下结论中不正确的为


A. 15名志愿者身高的极差小于臂展的极差
B. 15名志愿者身高和臂展成正相关关系,
C. 可估计身高为190厘米的人臂展大约为189.65厘米,
D. 身高相差10厘米的两人臂展都相差11.6厘米,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=etx(t>0),过点P(t,0)且平行于y轴的直线与曲线C:y=f(x)的交点为Q,曲线C过点Q的切线交x轴于点R,若S(1,f(1)),则△PRS的面积的最小值是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com