
| A�� | $\frac{23}{12}$ | B�� | 3 | C�� | 2 | D�� | $\frac{26}{11}$ |
���� ���õ����ļ�������������߷��̺�˫���ߵĽ����ߣ�������Ӧ�ķ���������������������Ķ�����������������ı���ʽ���������Թ滮��֪ʶ������⼴�ɣ�
��� 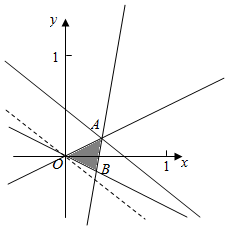 �⣺�����ĵ���f�䣨x��=3x2+2x+1��
�⣺�����ĵ���f�䣨x��=3x2+2x+1��
�����ڵ�M��1��4��������������Ϊk=f�䣨1��=3+2+1=6��
���Ӧ�����߷���Ϊy-4=6��x-1������y=6x-2��
˫���ߵĽ����߷���Ϊy=��$\frac{1}{2}$x��
���Ӧ�ķ������Ϊ��
��A��x��y������$\overrightarrow{OA}$•$\overrightarrow{OB}$=4x+5y��
��z=4x+5y����y=$-\frac{4}{5}x+\frac{z}{5}$��
ƽ��ֱ��y=$-\frac{4}{5}x+\frac{z}{5}$����ͼ���֪��ֱ��y=$-\frac{4}{5}x+\frac{z}{5}$��
������Aʱ��ֱ��y=$-\frac{4}{5}x+\frac{z}{5}$�ؾ����ʱz���
��$\left\{\begin{array}{l}{y=\frac{1}{2}x}\\{y=6x-2}\end{array}\right.$��$\left\{\begin{array}{l}{x=\frac{4}{11}}\\{y=\frac{2}{11}}\end{array}\right.$����A��$\frac{4}{11}$��$\frac{2}{11}$����
��ʱz=4x+5y=4��$\frac{4}{11}$+5��$\frac{2}{11}$=$\frac{26}{11}$��
��ѡ��D
���� ������Ҫ�������Թ滮��Ӧ�ã��漰�����ļ������壬˫���ߵ������Լ������������Ĺ�ʽ���ۺ��Խ�ǿ���������ϴ��������ν���ǽ������Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
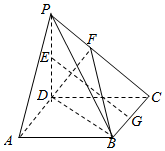 ��ͼ������P-ABCD�У�����ABCDΪ�����Σ�PD��ƽ��ABCD��PD=AB=2��E��F��G�ֱ�ΪPD��PC��BC���е㣮
��ͼ������P-ABCD�У�����ABCDΪ�����Σ�PD��ƽ��ABCD��PD=AB=2��E��F��G�ֱ�ΪPD��PC��BC���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2n-1 | B�� | 1-2n | C�� | 2-��$\frac{1}{2}$��n-1 | D�� | ��$\frac{1}{2}$��n-2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ${x^2}-\frac{y^2}{3}=1$ | B�� | ${y^2}-\frac{x^2}{3}=1$ | C�� | $\frac{x^2}{12}-\frac{y^2}{4}=1$ | D�� | $\frac{y^2}{12}-\frac{x^2}{4}=1$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [0��1�� | B�� | ��-�ޣ�-3�� | C�� | ∅ | D�� | ��-�ޣ�-3���ȣ�1��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com